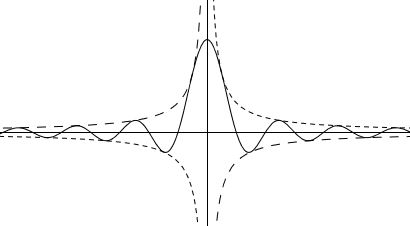
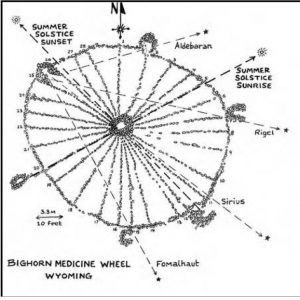
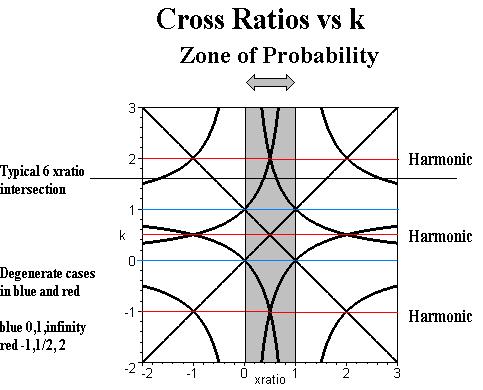
EU Meetup March 6, 2018
According to Euclid “A Ratio is a sort of relation in respect of size between two magnitudes of the same kind“.
A Magnitude is a Size: a property by which it can be compared as Larger or Smaller than other objects of the Same Kind. A Line has a Length, a Plane has an Area (Length x Width), a Solid a Volume (Length xWitdth x Height).
For the Greeks, the Numbers (Arithmoi) were the Positive Integers. The objects of Geometry: Points, Lines, Planes , were referred to as “Magnitudes” (Forms). They were not numbers, and had no numbers attached.
Ratio, was a Relationship between Forms and a Proportion was a relationship between the Part and the Whole (the Monad) of a Form.
Newton turned the Greek conception of Number completely on its head: “By Number we understand, not so much a Multitude of Unities, as the abstracted Ratio of any Quantity, to another Quantity of the same Kind, which we take for Unity”.
We now think of a Ratio as a Number obtained from other numbers by Division. A Proportion, for us, is a statement of equality between two “Ratio‐Numbers”.
This was not the thought pattern of the ancient Greeks. When Euclid states that the ratio of A to B is the same as the ratio of C to D, the letters A, B, C and D do not refer to numbers at all, but to segments or polygonal regions or some such magnitudes.
The Ratio of two geometric structures was determinated by fitting the Unit Parts of the first geometric Stucture into the Other.
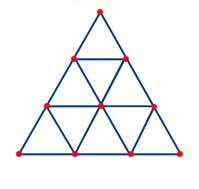
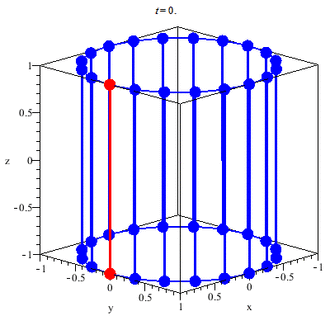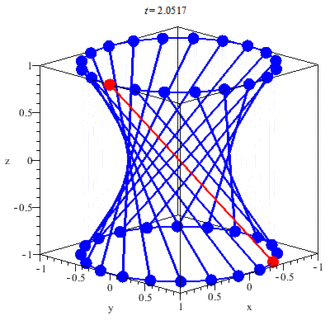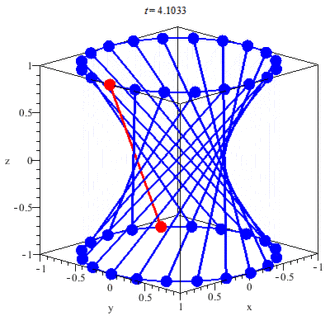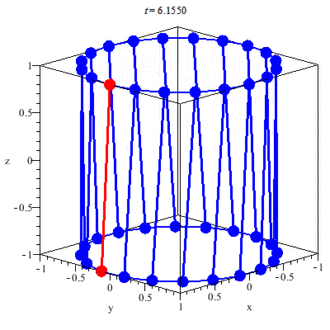
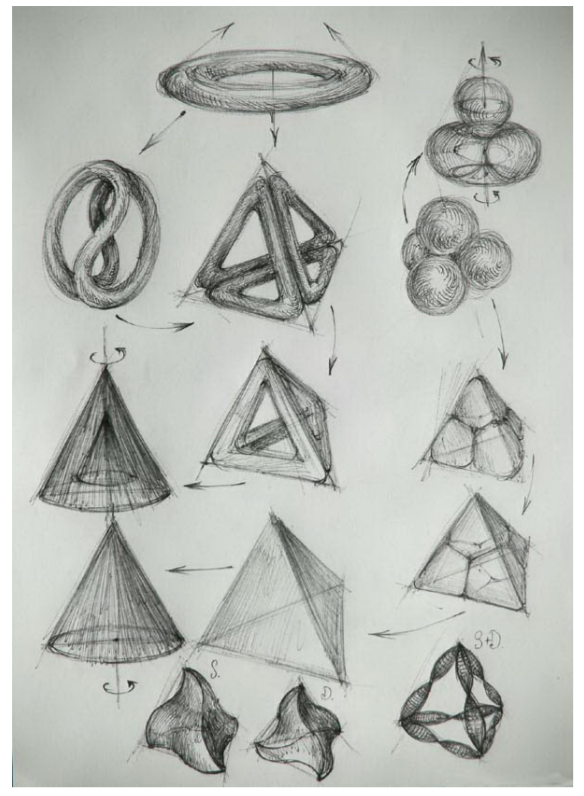
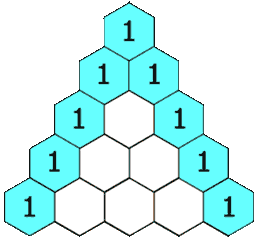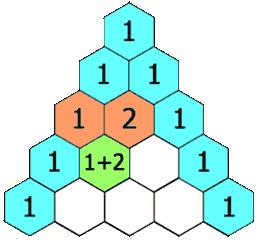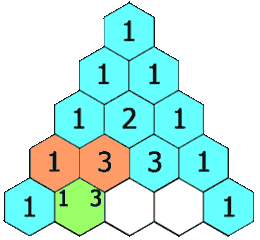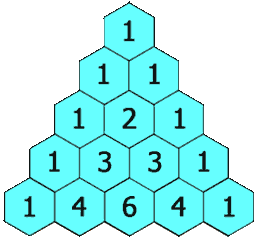
The Perfect Triangle of the Tetraktys contains 9 = 3×3 Triangels. A Triangle contains 3 Lines and 3 Points.
An Example: The Tetraktys is a Triangle (A Monad) and contains 9 Triangles (a Monad). The 1x1x1-Triangle Δ, a Part of the Tetraktys, is Proportional to the Whole of the Tetraktys (T) and has a Ratio T/Δ = 3= Δ -> T = Δ (3) x Δ (3) = 9.
The Mathematics of Euclid is not a Mathematics of Numbers, but a Mathematics of Forms.
The symbols, relationships and manipulations have Physical or Geometric Objects as their referents.
You cannot work on this Mathematics without Knowing (and Seeing) the Objects that you are Working with.
Geoffrey West - Natural Scaling - Time and Frequency
J. M. Boardman - NORTH SPIRIT: Mystical Insights
Fractal Field Physics Review-Dan Winter, FractalU.com 1st course 2018
About Mystical Number-Patterns
The Sēpher Yəṣîrâh (Book of Formation or Book of Creation, ספר יצירה) is the oldest book on Jewish Mysticism. The Sefer Yetzirah describes how the universe was created by the “God of Israel” through 32 Wondrous Ways of Wisdom.
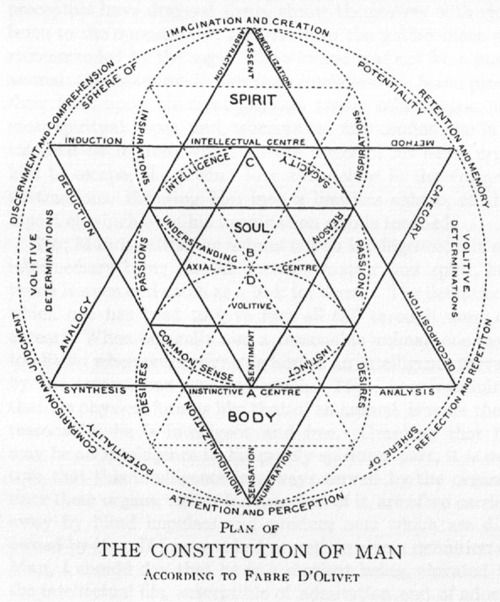
The Number 32 is the Sum of the 10 Sephirot and the 22 Letters of the Hebrew Alphabet.
The Sephirot is related to the Tetraktys of Pythagoras. The Tetraktys embodies the Four main Greek Cyclical (Platonic) Musical Harmonies: the Fourth (4:3), the Ffth (3:2), the Octave (2:1) and the Double Octave (1:4).
1+2+3+4 = 10. 10 is the 4th Triangular Number. The Nth triangular number is the Sum of the numbers 1 -> N. This Sum is equal to 1/2N(N+1).
Between the 10 Sephirot run 22 Channels or Paths which connect them.
The Sephirot are the Points of the Tetraktys. The Hebrew Letters are the Lines between the Points. The Lines of the Sephirot and the Tetraktys create a Cube (6) at the Top and a Tetrahedron (4) at the Bottom.
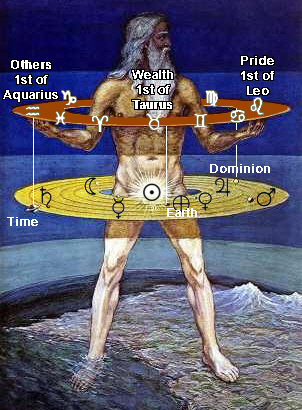
The Letters of the Hebrew Alphabet are divided in the 3 Mother Letters (אמש, the Trinity), the Seven Doubles (The Planets) and the Twelve Simples (the Zodiac).
The 22 letters of the Hebrew Alphabet are a combination of the Trinity, the 7 Planets and 12 Signs of the Zodiac.
When you analyse the Sepher Yeshirah the Cube of Space (the Kaaba) appears out of the Hebrew Alphabet. The Kaaba is related to the Seventh Planet, Saturn.
The following quote can be found in “The Power of Myth”:
If you follow your bliss, you put yourself on a kind of track that has been there all the while, waiting for you, and the life that you ought to be living is the one you are living. Wherever you are—if you are following your bliss, you are enjoying that refreshment, that life within you, all the time.
A lot of Campbell´s students obviously misinterpreted his quote as an advice to embrace hedonism as the path to happiness, to pursue “feeling good no matter what”. Late in his life and frustrated with this development, Campbell purportedly made the remark “I should have said, ‘Follow your blisters’.”
 xwdsc
xwdsc
-
https://m.facebook.com/story.php?story_fbid=1687537611292501&id=100001088353790
Method and device for transmitting the biological activity of a carrier material as a signal to another carrier material, and for processing said signal, and product thereby obtained
SCIENTIFIC CAREER
One of Wren's friends, another great scientist and architect and a fellow Westminster Schoolboy, Robert Hooke said of him "Since the time of Archimedes there scarce ever met in one man in so great perfection such a mechanical hand and so philosophical mind."
When a fellow of All Souls, Wren constructed a transparent beehive for scientific observation; he began observing the moon, which was to lead to the invention of micrometers for the telescope. He experimented on terrestrial magnetism and had taken part in medical experiments while at Wadham College, performing the first successful injection of a substance into the bloodstream (of a dog).
In Gresham College, he did experiments involving determining longitude through magnetic variation and through lunar observation to help with navigation, and helped construct a 35-foot (11 m) telescope with Sir Paul Neile. Wren also studied and improved the microscope and telescope at this time. He had also been making observations of the planet Saturn from around 1652 with the aim of explaining its appearance. His hypothesis was written up in De corpore saturni but before the work was published, Huygens presented his theory of the rings of Saturn. Immediately Wren recognised this as a better hypothesis than his own and De corpore saturni was never published. In addition, he constructed an exquisitely detailed lunar model and presented it to the king. Also his contribution to mathematics should be noted; in 1658, he found the length of an arc of the cycloid using an exhaustion proof based on dissections to reduce the problem to summing segments of chords of a circle which are in geometric progression.
A year into Wren's appointment as a Savilian Professor in Oxford, the Royal Society was created and Wren became an active member. As Savilian Professor, Wren studied mechanics thoroughly, especially elastic collisions and pendulum motions. He also directed his far-ranging intelligence to the study of meteorology: in 1662 he invented the tipping bucket rain gauge and, in 1663, designed a "weather-clock" that would record temperature, humidity, rainfall and barometric pressure. A working weather clock based on Wren's design was completed by Robert Hooke in 1679.
In addition, Wren experimented on muscle functionality, hypothesizing that the swelling and shrinking of muscles might proceed from a fermentative motion arising from the mixture of two heterogeneous fluids. Although this is incorrect, it was at least founded upon observation and may mark a new outlook on medicine: specialisation.
Another topic to which Wren contributed was optics. He published a description of an engine to create perspective drawings and he discussed the grinding of conical lenses and mirrors. Out of this work came another of Wren's important mathematical results, namely that the hyperboloid of revolution is a ruled surface. These results were published in 1669. In subsequent years, Wren continued with his work with the Royal Society, although after the 1680s his scientific interests seem to have waned: no doubt his architectural and official duties absorbed more time.
It was a problem posed by Wren that serves as an ultimate source to the conception of Newton's Principia Mathematica Philosophiae Naturalis. Robert Hooke had theorised that planets, moving in vacuo, describe orbits around the Sun because of a rectilinear inertial motion by the tangent and an accelerated motion towards the Sun. Wren's challenge to Halley and Hooke, for the reward of a book worth thirty shillings, was to provide, within the context of Hooke's hypothesis, a mathematical theory linking the Kepler's laws with a specific force law. Halley took the problem to Newton for advice, prompting the latter to write a nine page answer, De motu corporum in gyrum, which was later to be expanded into the Principia.
Mentioned above are only a few of Wren's scientific works. He also studied other areas, ranging from agriculture, ballistics, water and freezing, light and refraction, to name only a few. Thomas Birch's History of the Royal Society is one of the most important sources of our knowledge not only of the origins of the Society, but also the day to day running of the Society. It is in these records that most of Wren's known scientific works are recorded.