The first key to taking the wheel to the next dimension is the six hexagrams, and the triangles they contain.
We will always count the numbers on a triangle clockwise in order to label them. Think of this as the experience of time in one direction. It is helpful, however to think of a backwards stream of information through time. Thus we have 3-6-9; 6-3-9; 1-1-1; 8-8-8; 1-4-7; 5-2-8; 1-7-4; 2-5-8.
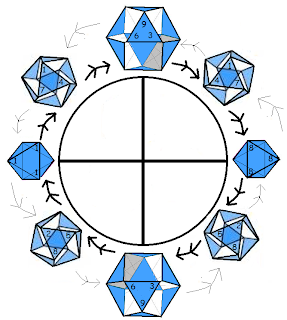
The next key I discovered is the application of the Buckminster Fuller Vector Flexor “jitterbug”. This is a beautiful geometric dance which Bucky believed was a model for the Universe. It is significant I think, because it shows the crucial transformation from cubic/octahedral symmetry to dodecahedral/icosahedral symmetry. Take a look at these animations to get an idea of how this works.
Our starting point will always be the cubeoctahedron, which is known in physics as vector equilibrium.
This will correspond to the first two triangles, 3-6-9 and 6-3-9. This also corresponds to a noble gas in Walter Russel’s system (diagram in my post Template for Universal Mathematics): asexuality, maximum inertia, maximum stablitiy, maximum complexity/softness of crystallization.
The cubeoctahedron then can tilt to the right or left, where it becomes an icosahedron at a tilt of 15 degrees. This is the same tilt angle as the four askew triangles, 1-4-7; 5-2-8; 7-4-1 and 2-5-8!!! When the icosahedron is closing into the octahedron, it is male, and when it opens back into the cubeoctahedron it is female.
At the maximum point of the wave, the figure collapses to an octahedron. This corresponds with carbon: bisexuality, maximum compression, maximum resistance, simplicity and hardness of crystallization, and the appearance, due to motion, of the stability of form.
Despite the 3-dimensional transformation between these three shapes, a 2-dimensional hexagram is visible, when we center our perspective on a triangular face. So we see a motion which moves in a cycle, but can change direction at four turning points: 9-6-3; 3-6-9; 1-1-1; and 8-8-8. In this way, it can be steered into infinitely complex forms. We can look at it like a flow chart indexed by the angle of the triangle that is front and centered, corresponding with the 8 triangles of our 24 number circle.
Now compare this with the eight trigrams around a circle which form the basis of the I Ching.
The four trigrams at the top/bottom/left/right are in positions of relative balance, at the zero points and peaks of the wave, whereas the four trigrams at diagonals are in the transitional phase. Because the left side of the circle is a mirrored inverse of the right side, we can unite the opposing hexagrams for a deeper understanding of this system. The noble gas is both Creative AND Receptive, it contains both the memories of every action, and the imagination which will create the future. The dense matter of maximum potential at the peak of the wave is Radiant AND Dark. That is, hot and cold, light and dark, dense motion at the center and tenuous space surrounding it are in maximum opposition. We can simplify and bring these two together into a kind of magic square/circle.
3-6-9 triangle becomes 3 according to multiples of 3; likewise 6-3-9 becomes 6. 1-1-1 becomes 1, 8-8-8 becomes 8. 1-4-7 becomes 4 because it is powers of 4, and 7-4-1 is powers of 7. 2-5-8 and 5-2-8 are abbreviations of halving and doubling cycles, or 5 and 2, respectively.
Now imagine that you can not only change direction from clockwise or counter-clockwise, but that, at any stage of the cycle, you can choose a new center triangle to start from. This gives us a model of the 4-dimensional 24-cell, which can nest all five platonic solids. Look at this view where the octahedron goes from a plane, to fully formed, back to a plane again.
To view it as a 3-d hologram, cross your eyes and try to bring the two images into resolution together, a lot like a Magic Eye. I recommend printing the image if you are doing this a lot, as staring at a computer screen with your eyes crossed will give you a headache. From this page on Hyperspace. http://home.comcast.net/~eswab/hyprspac.html
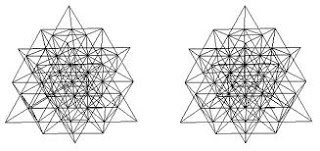
Furthermore, it unfolds the pattern to 64 total permutations, just like the I Ching. If this can be shown to be a workable system, it would throw a completely new spin (literally) on the I Ching; there are various states of motion described by the different hexagrams. From this perspective, we could use Nassim Haramein’s 64 tetrahedron vector-matrix grid ( http://www.theresonanceproject.org/graphics.html ) as a starting point. I am trying to find someone who could model this matrix going through the Vector Flexor Jitterbug Dance.
More to come, feedback is encouraged/appreciated. Peace to All.
Rodin Fibonacci Wheel Symmetries
I would like to take a slightly deeper look at the Fibonacci/Rodin number wheel. But first, a quick review of Marko Rodin’s vortex based mathematics for those that aren’t so familiar. It is based on reducing all numbers to whole numbers, for example 25 = 2+5 = 7 or 1.156 = 1+1+5+6 = 13 = 1+3 = 4. From this we see very interesting patterns emerge. It may seem simple at first, but I believe it has far-reaching applications some of which we have seen in the development of the Rodin Coil. Take a look at this simple multiplication table – thanks to Chris Te Nyenhuis for this.
Now we turn to the Fibonacci wheel. The Fibonacci numbers were known in India as far as the 6th century, but Italian mathematician Leonardo Fibonacci introduced them to the West in the 12th century. They are formed by adding two consecutive numbers in the series to get the next one. The first few are 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… We see this series everywhere in nature, including the geneology of bees, the growth of pinecones and sunflowers, and even the relative orbit of Earth and Venus http://www.takayaiwamoto.com/Earth_Moon_Sun/Harmony_Planets.html. The Fibonacci series can be thought of as a whole number expression of the all-important Golden Ratio, as the ratio between numbers in the series comes closer to approximating phi = 1.61803399…
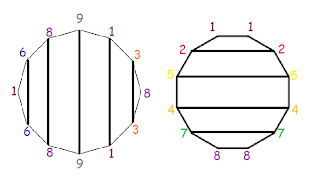
Watch what happens when we run the Fibonacci series as Rodin numbers. We get a sequence of 24 numbers, then the sequence repeats! We can run these numbers round a 24-sided wheel, where we see very interesting symmetries.
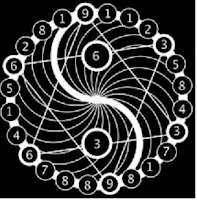
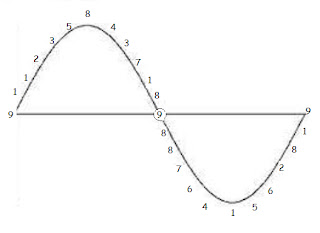
First off, we notice that each number is directly opposite its inverted pair. This allows us to look at the cycle as a sine wave. When the wave dips down, all the numbers repeat themselves but become inverted, subtracted from 9. 1, 1, 2, 3, 5… is mirrored in 8, 8, 7, 6, 4…
9 is 0, and 1 and 8 are the points of maximum potential. So the Fibonacci Series maps out a sine wave. Does this give us an insight into the true spiraling nature of the wave?
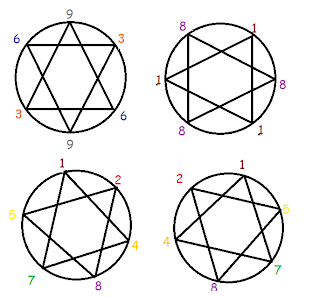
This 24 number circle can also be divided into 4 hexagrams.
Template for Universal Math and Geometry
This model, which is still in its early Evolution, is the result of a synthesis many different streams of information that are resurfacing in this age of information explosion. Some of these sources are fairly obscure, but currently resurfacing as a result of the Times we live in. Nonetheless, I believe there is potential to make this a very elegant, simple, working model with applications from computers to chemistry. I will be taking time later to flesh out the various ideas presented and how they correlate.

These numbers are formed from the Fibonacci series, a sequence of whole numbers which increasingly approximate the Golden Ratio. Using Marko Rodin’s Vortex-Based Mathematics (http://markorodin.com/1.5/), we add up the Fibonacci numbers into single digits, and a very clear pattern emerges. The numbers occur in a repetitive cycle of 24, which can be arranged around a circle, where one who is familiar with Rodin numbers immediately will notice the patterns.
Notice the 9 at each node, which are points of two 3-6-9 triangles moving clockwise and counter-clockwise. Notice also how each number added to the number directly across from it is equal to 9. Thus the cycle can also be looked at as a sine wave with 9 at zero, and the two sides of the circle as mirror inverses of each other. The other triangles formed are the 1-4-7 and 2-5-8 families going both clockwise and counter-clockwise, and a 1-1-1 triangle and 8-8-8 triangle. More on this as it relates to crystallization later.
Now compare all this to the Law of Crystallization provided by Walter Russell in his magnum opus The Universal One.