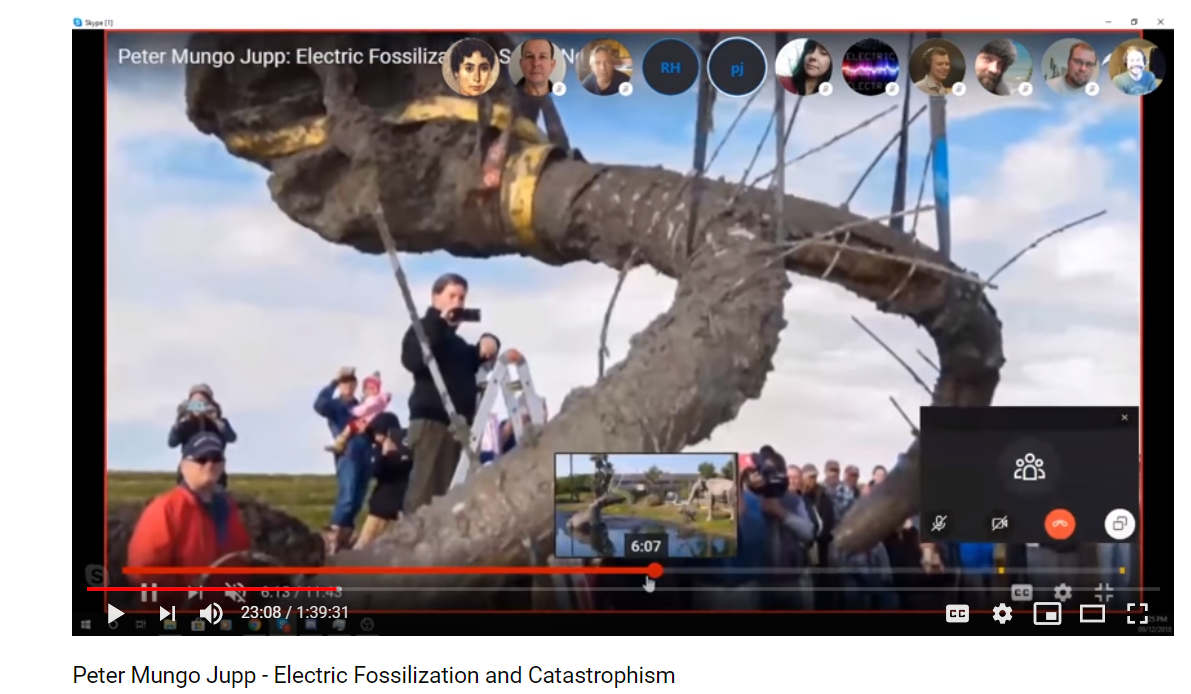
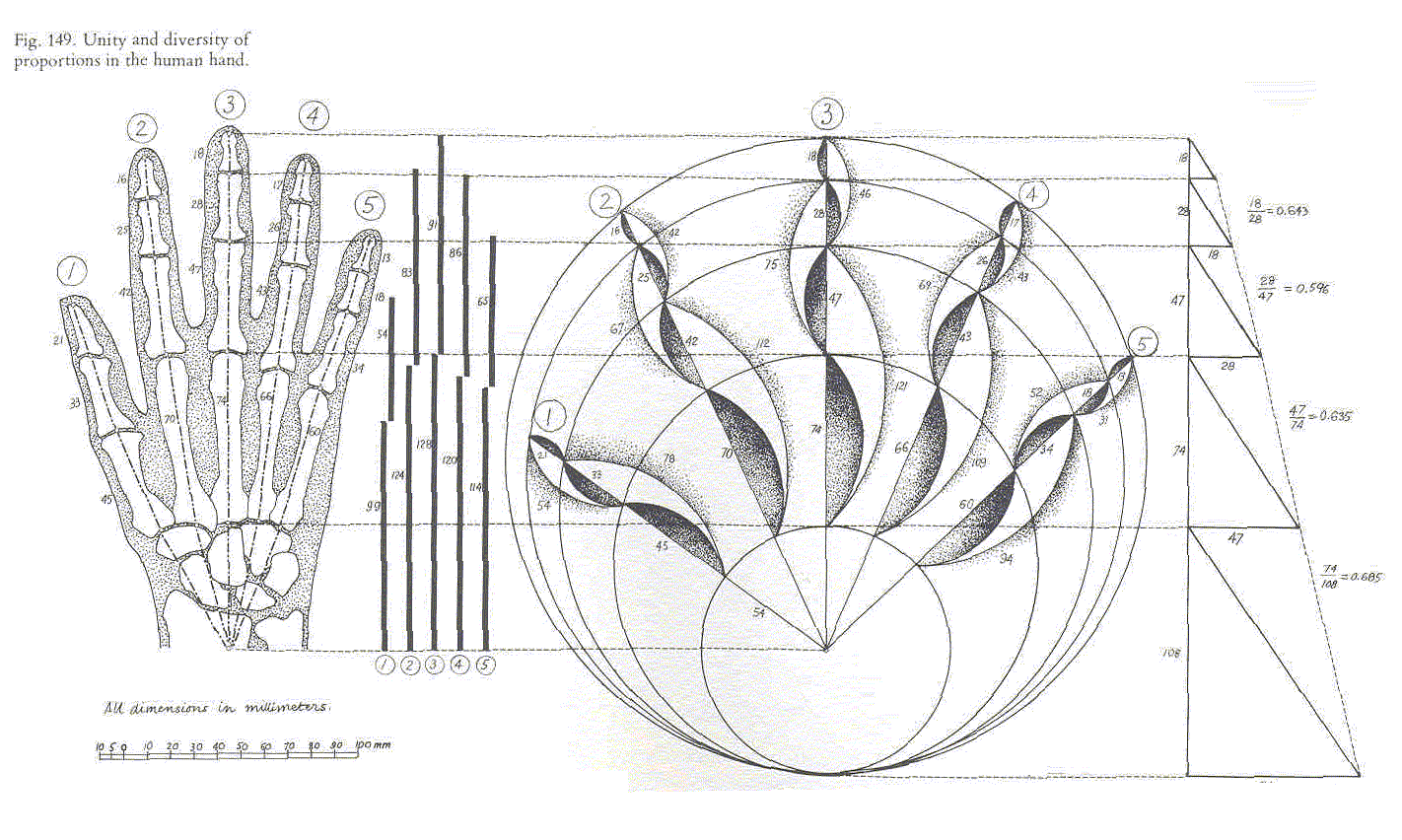
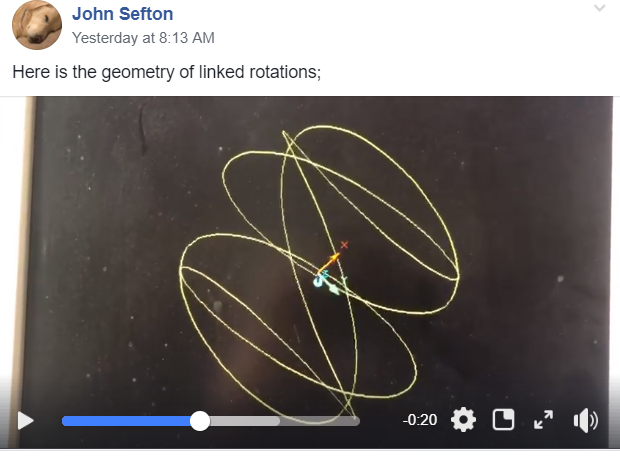
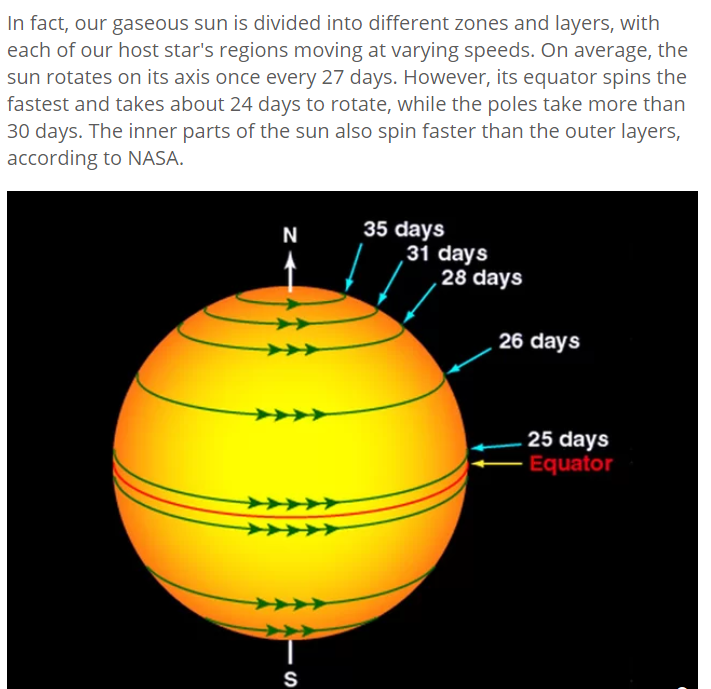
062 EU Meetup December 18th 2018
Ignacio Cisneros – Images from EU Skype Group
A further and related blow to the statement centered
empiricist account of meaning arose from
studies in the history of science. Empiricists held
science to be the paradigm of rational inquiry. On
this model, both individual beliefs (e.g., scientific
hypotheses) and whole theories were accepted or
rejected by comparing statements implied by a
theory against what experience reveals. However,
the history of science manifests a rather different
picture of this relationship between experience and
belief. Indeed, the historical picture reverses the
order of knowing assumed by empiricism. Belief
determines what in perception is correct and not
vice versa. As a consequence of the interdependence
of statements discussed above, theories
shaped the very perception of what might count as
evidence. One could not observe microbes by looking
through a microscope if one had no way of
integrating what one observes into a more informed
understanding of these observations as those things.
Nothing in the mere act of looking determines
foreground and background, items of significance
from mere “noise.”
061 EU Meetup December 11th 2018
060 EU Meetup December 4th 2018
059 EU Meetup November 27th 2018
058 EU Meetup November 20th 2018
057 EU Meetup November 13th 2018
https://youtu.be/ALqQDROygF0
In 1929 Hubble published his works describing red shift was related to velocity. But he then spent the next 25 years attempting to dispute his own work. No one listened, an expanding universe is necessary for accepting special relativity. Hubble was ignored.
Halo Substructure in the SDSS-Gaia Catalogue: Streams and
Clumps