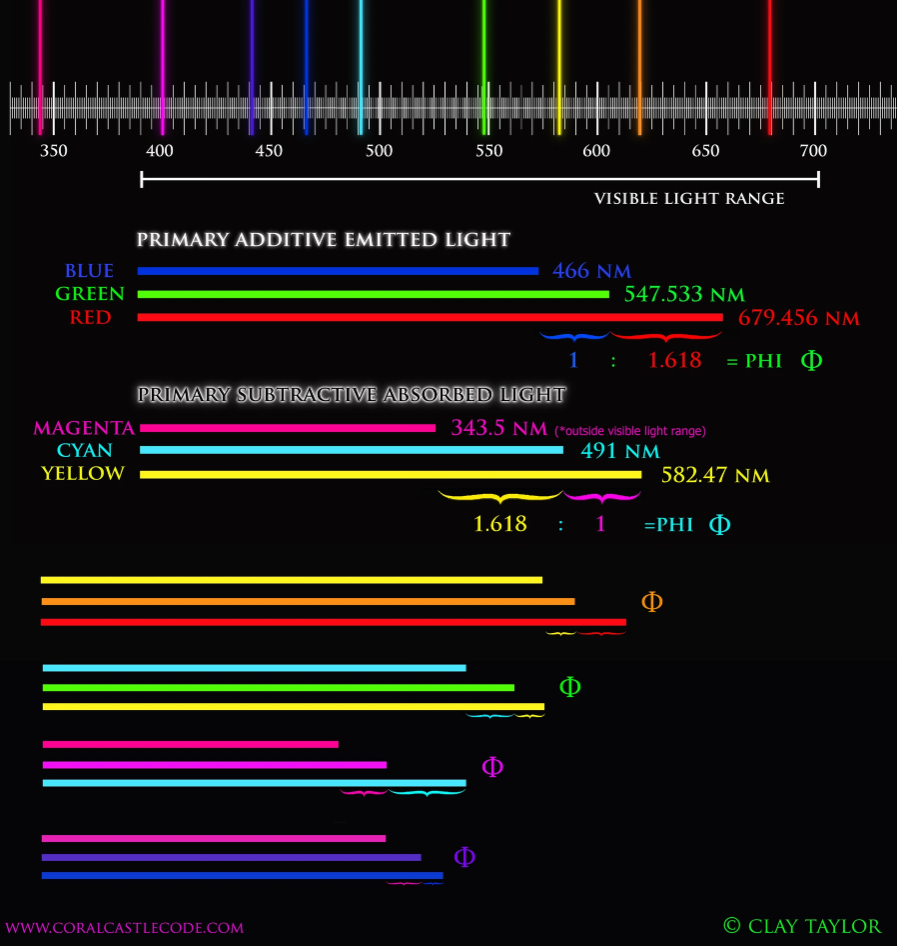
A TALE OF TWO RATIOS
“While I understand all ratios to be mathematically interrelated, if one were to ask me what I would consider to be the most fundamental ratios of all, my answer would be the Octave (doubling and halving) and Phi, represented by the symbol Φ. (It is assumed the reader is already familiar with the basics of these values.)
These two ratios are known to be related in ways that may be described geometrically, but in terms of the timing and spacing of vibrations, they are very practically opposites. The octave clearly exists in the realm of utterly rational whole numbers (1,2,4,8 and on) while Phi is considered “the most irrational number.” From one, it immediately strays from wholeness and no successive iteration of Phi (1.618…) will ever return to wholeness (unless of course, as the reader should be aware, it is multiplied by its counterpart, in this case phi, represented by the symbol φ, 0.618… which returns it to 1.)
In the realm of sound vibrations for instance, the Octave makes it clear that doubling and halving of a fundamental tone retains the tonal quality of that fundamental. Even while it now exists in a higher or lower pitch, it is in essence the same key which may be repeated to infinitely higher or lower intervals. Thus, the Octave is effectively the most harmonic interval possible. In contrast, a note that is a value of phi from that fundamental will never truly reach the original tonal quality of the root/ tonic/ fundamental reference tone, even within an eternity of iterations. Another way to imagine this is that if Phi rotated around a clock, starting at noon, due to its incommensurability it will never hit exactly noon ever again, no matter how many times you turned it by this value. In contrast, the Octave would hit 1:00 every single time (in its doubling direction.)”