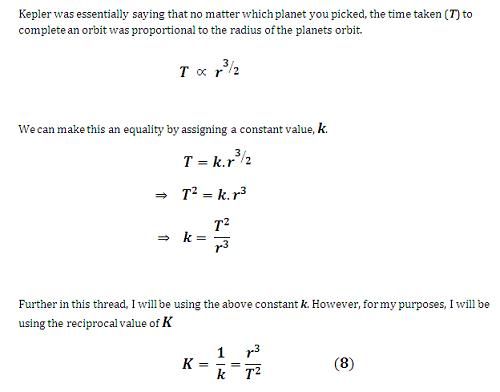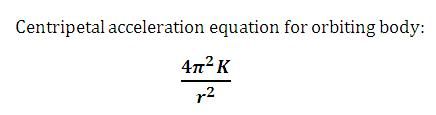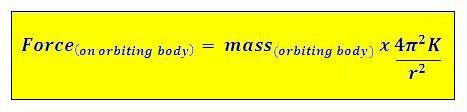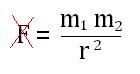Allow me to open this thread by asking you a very simple and straightforward question:
"What keeps the moon in orbit around the earth and the earth in orbit around the sun ?"
Most likely you answered, as I once did, that it's obviously gravity that keeps both the moon and the earth in their respective orbits around their primaries. It's just so obviousthat you're also wondering why I'm even bothering to ask such a question !
The reason I'm asking was prompted by my attempt to help my son with his science homework regarding how the moon orbits the earth, it's distance from earth, it's velocity as it orbits earth, etc. In the process of explaining the basic concept using readily available planetary data tables, I noticed something quite unusual and unexpected ... at least to me.
However obvious gravity as an explanation may seem to be, now I'm not nearly so sure as I used to be that the answer is so simple and straightforward and in this OP, I'll try to provide evidence to back up and substantiate my belief that gravity plays NO part in causing a moon to orbit a planet or a planet to orbit a sun.
The understanding that the force of gravity was the primary mechanism responsible for restraining the moon in it's orbit around the earth (and the earth in it's orbit around the sun) has been a mainstream and unchallenged principle of physics ever since Newtonpublished his now famous Law of Universal Gravitation way back in 1687.
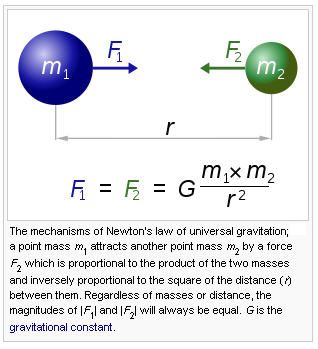
This law essentially states that every particle in the universe attracts every other particle in the universe with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
Mathematically, this concept is expressed by this equation:
and here's an image to help get a more visual 'feel' for what this law is saying:
Ok, so far ? Fairly straightforward as taught in virtually all high school physics classes.
Newton was simply referring to a couple of objects such as planets, moons, etc and the distance between them. The only term in the equation that may cause some confusion is the G term that represents what's known as the Gravitational constant and basically was a scaling factor that had to be introduced to make the Law of Universal Gravitation work. More will be said about this constant later.
So how did this famous law come into existence ? How did Newton arrive at a definitive mathematical statement that claimed that yes, there was indeed an 'attracting force' operating in the universe when prior to his formulation, there was only a vague suspicion that something similar to an 'attracting force' was occurring ?
Newton based his work on that of the German astronomer Kepler who preceeded him. Kepler had accumulated a large quantity of observational data relating to the movement of the planets and based on this empirical data in conjunction with data derived even earlier by the Danish astronomer Tycho Brahe, eventually formulated a number of laws giving an approximate description of the motion of planets around the Sun.
Kepler's laws are:
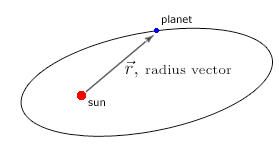
- The orbit of every planet is an ellipse with the Sun at one of the two foci.
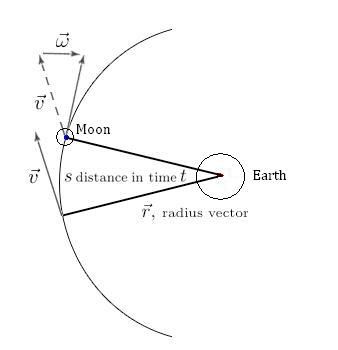
- A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.
- The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.
Kepler's 1st law can be visualized this way:
Kepler's 2nd law can be visualized this way:
The above served as the framework and basis for Newton's intellectual leap forward in giving the concept of a "gravitational force'" that had only been suspected and gave it now a solid and indisputable mathematical, and therefore, universally accepted legitimacy within mainstream physical science.
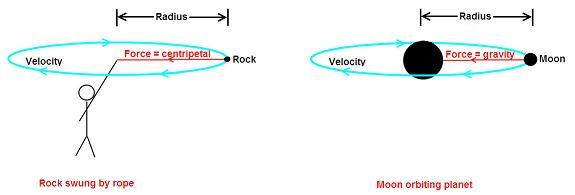
Newton would have been perfectly justified in assuming there was a similar mechanism and therefore principle, operating in the observation of the moon orbiting around the earth to that of a rock being swung around on the end of a rope by a person. In the case of the rock, the constraining force causing the rock to follow a circular path, or orbit, around the person was the tension in the rope connecting the person to the rock. For the moon, he would have reasoned that there must have been an analogous force to the rope, connecting the moon with the earth and constraining the moon to follow a circular path, exactly as the rope forced the rock to do.
In the case of the rope and rock, Newton was well aware of the concept of a centripetal force that makes a body follow a curved path.This force is always directed inward toward the center of curvature of the path.
So an obvious comparison would be as follows
in which case it would have been a justifiable comparison to equate the centripetal force on the rock to that of the gravitational force acting on the moon.
In essence, that's exactly what Newton did. He derived a formula for the centripetal acceleration of the orbiting body and inserted it into another of his famous Laws that states:
Second Law: A body of mass m subject to a force F undergoes an acceleration a that has the same direction as the force and a magnitude that is directly proportional to the force and inversely proportional to the mass, i.e., F = ma.
Once Newton had a "centripetal acceleration" equation, he replaced the a in the F = ma equation, did some additional mathematical manipulations and eventually arrived at an equation that apparently seemed to describe a "real" force that exists between masses such as planets, moons, suns, etc.
However, Newton found that to make this equation "work" and produce "reasonable" answers, he was forced to introduce a mysterious constant into the equation. This constant eventually became known as G or the Universal Gravitational Constant ... without this G constant, Newton's equation fails to work.
Ok, what I'm about to do is use Kepler's 3 Laws to firstly, derive my own centripetal acceleration equation ... then having done that, use my centripetal acceleration equation to derive an equation that also EXACTLY produces the very same results as does Newton's famous equation with 2 very significant differences.
The 1st difference is that I completely eliminate the need to have a mysterious "gravitational constant" in my equation, and the 2nd difference being that I eliminate the need to use the sun's mass entirely. So, in summary, Newton uses the mass of the sun and a planet but I need only the mass of the planet ... Newton needs to use a mysterious constant to make his equation work but I don't.
Ready ? Ok, let's get to it
Firstly, we need to determine an equation that will give us the centripetal acceleration acting on an orbiting body such as a planet or moon ... I'll do my best to keep the maths simple, straightforward and hopefully easy to follow !
At this point we have ourselves an equation that gives us the centripetal acceleration acting on an orbiting body based solely on the distance between the orbiting body and the object being orbited; and the time taken to complete the orbit.
This equation would be even more useful (and simpler) if we could get rid of the time factor (T) entirely from the denominator. Well, thanks to Kepler we can. Using Tycho Brahe's painstakingly collected data, Kepler was able to deduce that no matter which planet you picked, the ratio of the planets orbital radius to it's total orbital time always gave the same value ... in other words a constant. Essentially Kepler found that the total time period to complete an orbit is proportional to the 3/2 power of radius for all planets.
I'll now use the above information to simplify the previously derived centripetal acceleration equation.
Now we can use the K constant just derived and use it to simplify the centripetal acceleration equation from (7).
It's taken a while (and a little bit of maths
) but we have now arrived at a point where we have an extremely simple equation that describes the centripetal acceleration force acting on ANY orbiting body ... whether that happens to be a planet orbiting the sun or the moon orbiting the earth ... and it applies to all orbits anywhere in the universe.
Take a good look look at the centripetal acceleration equation describing the result of a 'force' acting on the orbiting body and causing it to follow a circular orbital path.
Essentially it is stating that the observed orbital centripetal acceleration ENTIRELY depends upon the distance (r) of the orbiting body from the body being orbited.
There is no mention whatsoever of either the mass of the orbiting body or the mass of the body being orbited ... and definitely NO mention of a gravitational force !
In fact, mass and a gravitational force are completely superfluous !
Ok, we now have ourselves an equation describing the centripetal acceleration being experienced by an orbiting body. The final step is to take Newton's 2nd Law (F=ma) and replace the a term with my centripetal acceleration equation ... giving ...
As you can see, the equation uses ONLY distances, time (contained within the K value), and a single mass.
No need for a mysterious gravitational constant .. no need for a second mass.
Ok, lets now do some examples and compare Newtons answers with mine
Example 1: Calculate the force between the sun and mercury:
We'll do it Newton's way 1st.
Now, my way ...
Well, look at that ... virtually identical results !
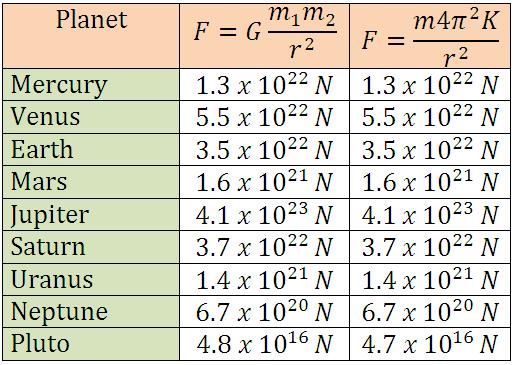
And just to show that I didn't cherry pick the example or that it was a fluke, I'll calculate the remaining planets and display Newton's and my results in table form.
As can be seen from the results displayed in the above table, the force values obtained from Newton's equation when compared to the force values obtained from my alternative equation are for all intents and purposes ... IDENTICAL.
But as I have just demonstrated, the requirement for a second mass and a mysterious "gravitational constant" are COMPLETELY SUPERFLUOUS.
Both Newton's equation and my alternative equation give results in the correct dimensions of "force", namely
However, my alternative equation gives the result immediately in the correct force dimensions without the need for a constant. This is not the case with Newton's equation where it was necessary to provide a "gravitational constant" so his results could be manipulated into the correct format of "force".
If the gravitational constant (G) is removed from Newton's equation so it looks like this
the results from this equation are no longer in force dimensions.
So, it's very apparent that the primary purpose for Newton needing to invent and include this gravitational constant (G) was to "manipulate or fudge" the otherwise incorrect results his equation would have given and convert them into the correct dimensions of force.
Ok, that's enough for the time being as I'll have more to say in a forthcoming 2nd part to this thread's topic.
I've checked, double and triple checked my logic and it seems to be sound ... but that doesn't mean that I haven't made silly errors that have sneaked past me that I haven't caught and consequently invalidate this thread. So please feel free to rip into it, tear it apart and comment on any obvious (or not so obvious) errors in the logic that I've detailed above.