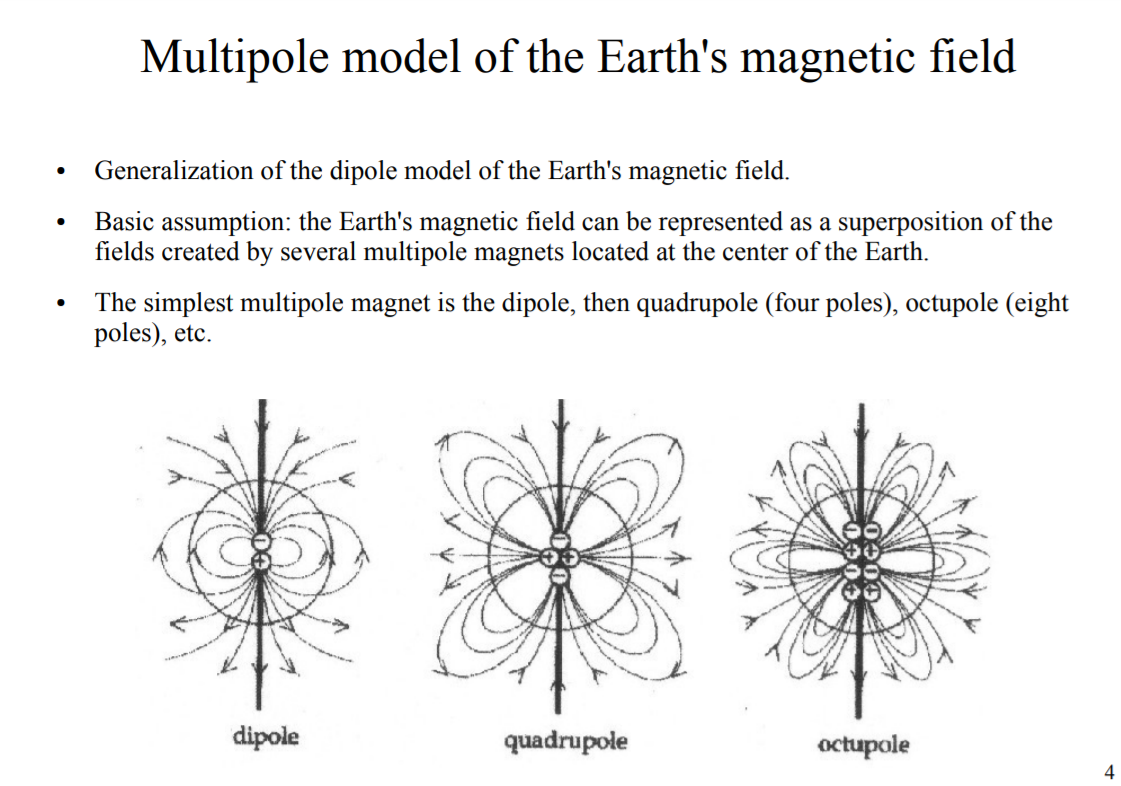
Gary Doskas - Spherical Harmony

Gary Doskas graduated with a Bachelor’s degree in Electrical Engineering from Concordia University in Montreal, Quebec Canada in 1984. Has been working in the semiconductor industry for 27 years. Since April 2010, he has been researching (self-taught) structural shapes within a spherical geometric context. His book, ‘Sphere of Life VI: The Harmonic Relationships of Cones, Spheres, and Platonic Solids’, was published in Jan 2011.

Let’s assume some two-dimensional world has evolved to a point where it consists of an infinite number of two-dimensional shapes constructed from sheets of zero thickness. This world would consist of polygon and elliptical shapes of all sizes. How could this world evolve or transform itself into a three-dimensional world? I will conclude this book with postulating the following theory on the evolution of the polyconix.

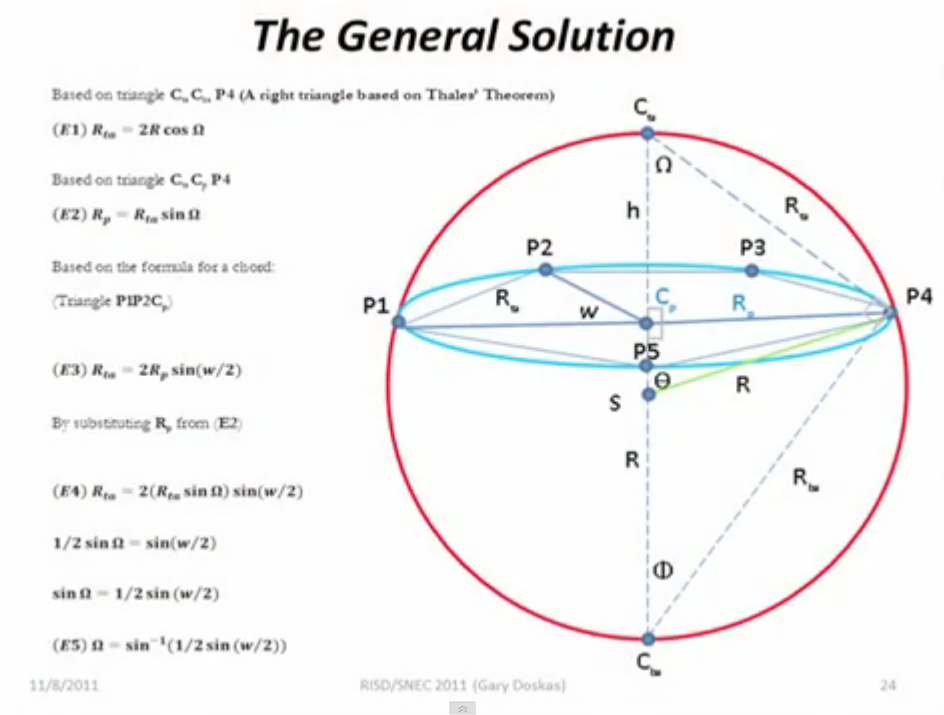
What is remarkable about these geometric relationships is that they can be experi-enced through pure geometric construction using just a compass. This can easily be experienced by both the young and mathematically inexperienced people. Knowledge of spherical trigonometry is NOT required and only basic trigonometry is required to explore the more complex relationships in more detail.

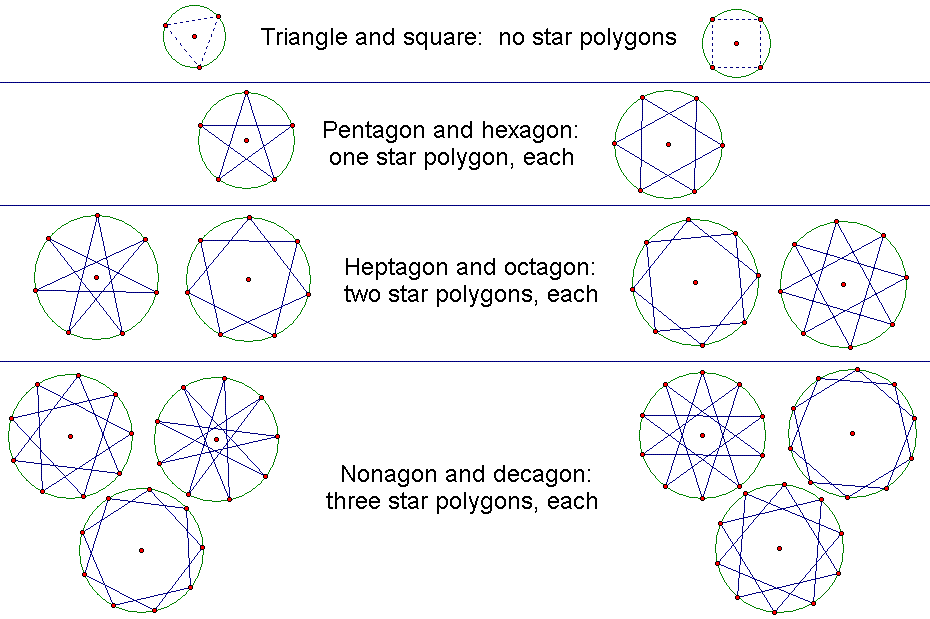
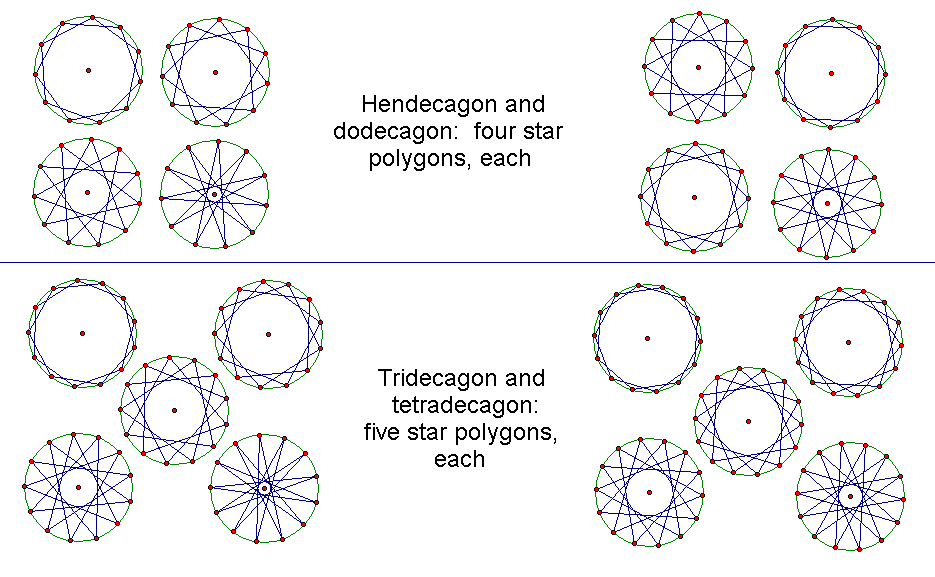
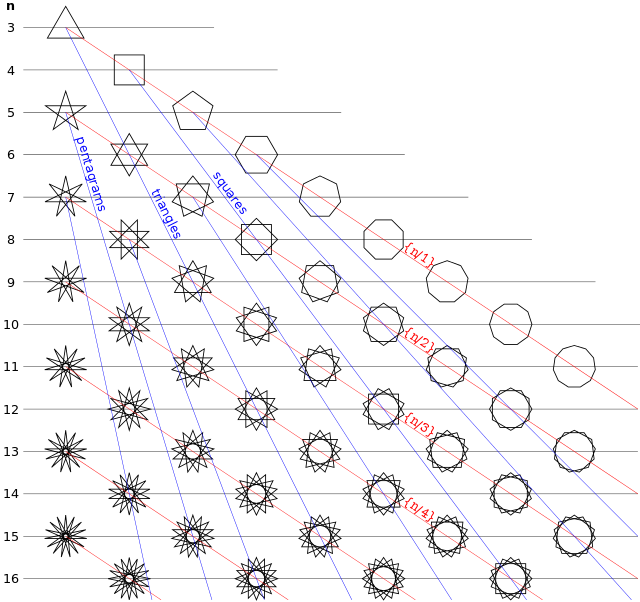
This book has its roots in a previous publication of mine, Spherical Harmony: A Journey of Geometric Discovery. I will introduce the concept of spherical harmonics, but the main focus will be on fractional harmonics and their associated polygram, or star polygon. There exists a unique fractional harmonic of each of the infinite number of star polygons. Much has been written about the pentagram and the golden ratio that is embedded in its geometry. However, it was the heptagon and associated heptagram that really piqued my interest. So I decided to explore the heptagram since I didn't know much about its geometric properties or characteristics and there wasn't much written about them either. The prime number seven has a special place in the ancient world and was referred to as the virgin number and was the most sacred number in many religions. some amazing ratios of proportion.

Instead of taking the classical approach of breaking down larger objects (molecules/atoms and protons/neutrons/electrons) into their smaller constituent parts (quarks, leptons, and bosons), I will take a different approach to describe the origins of the universe based on a simple geometric model. I will start with defining a particle with the smallest radius imaginable and describe their geometric evolution to larger particles.

Spherical Harmonic Expansion of the Earth’s Magnetic Field