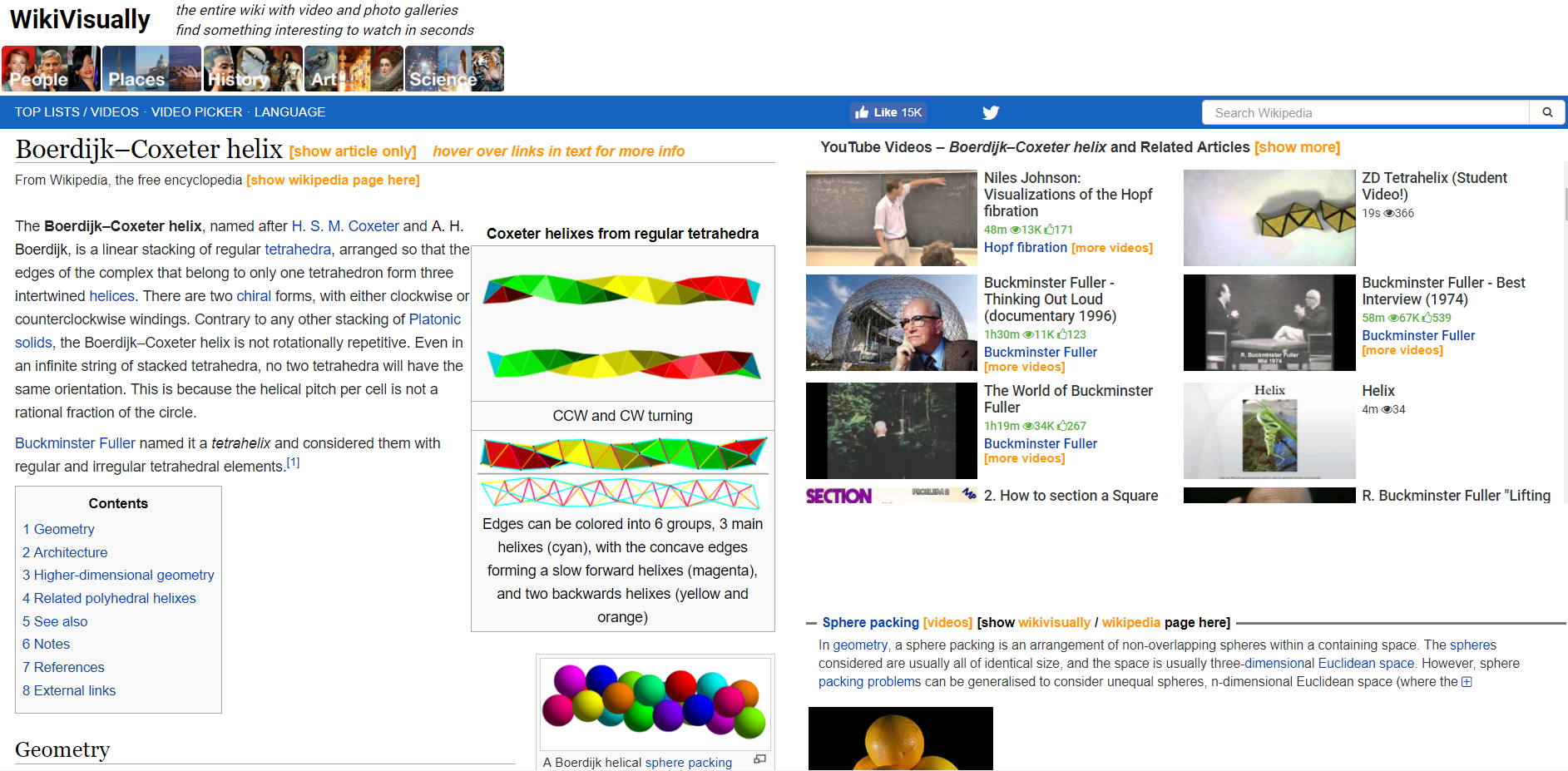
The radius of the cylinder will be
where EL is the edge length of the tetrahedra used to build the tetrahelix.
Let us put a vertex (call it V0) of one of the tetrahedra on the x-axis. That is
Then the next vertex of the tetrahelix (V1) will be at the coordinates
where theta is the angle around the z-axis and is given by
and where h is the distance in the z-axis direction and is given by


In the above figures, the yellow band connects a vertex to the "next" vertex, while the distance h is the distance between the 2 blue bands around the cylinder.
In general, the coordinates for the vertices of a Counter Clockwise tetrahelix Vn (n = 0, 1, 2, 3, ...) are given by
The coordinates for the vertices of a Clockwise tetrahelix Vn (n = 0, 1, 2, 3, ...) are given by
Note that cos(theta) = -2/3 and that sin(theta) = sqrt(5)/3. You can calculate exact expressions for the vertex coordinates by using these relations together with the following trig identities:
sin(n*theta) = sin(theta)*cos((n-1)*theta) + cos(theta)*sin((n-1)*theta)
One of the reasons that deriving the above information is difficult is that the axis of symmetry of the cylinder (the axis through the center of the cylinder) does not pass through the center of volume of the tetrahedra. The distance from the z-axis to the tetrahedron center of volume is given by the equation
Therefore, all the Tetrahelix cylinder axis of symmetry pass tangentially by a sphere of radius (sqrt(2)/10)EL centered at the Tetrahedron's center of volume.
Comments
- Tetrahelix come in 2 orientations; a right-handed spiral and a left-handed spiral.
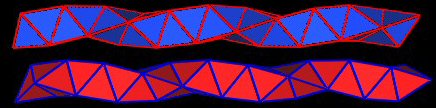
- The vertices of the tetrahelix never line up. That is, no two vertices will ever be directly above one another. This is because the theta angle above is an irrational number.

- It looks like you might be able to "nest" 3 additional tetrahelix about the original tetrahelix in a nice tight bundle. But this is not possible. The reason is that face binding 5 tetrahedra together about a single edge/axis leaves a gap (which Fuller calls the unzipping angle.) The dihedral angle of the regular tetrahedron is
5 times this amount is approx 352.643895 degrees which is approx 7.356105 degrees (the unzipping angle) short of 360 degrees. So the tetrahedra of multiple helixes can not pack together without gaps.
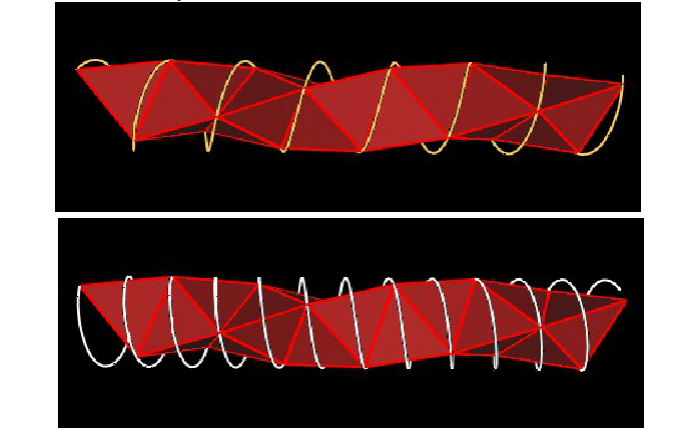
There are 12 possible Tetrahelix passing through a single Tetrahedron: 6 Clockwise and 6 Counter clockwise. As the figure shows, the spiral/coil associated with a Tetrahelix going through a Tetrahedron passes through all 4 vertices of the Tetrahedron sequentially. Since the spiral has the same symmetry axes as the Tetrahelix, we can count the number of possible different spirals to count the number of Tetrahelix.

We label the Tetrahedron's vertices by numbering them 1, 2, 3, and 4. Then there are 4x3x2x1 = 24 combinations for the order in which the spiral can pass through the vertices. However, 1/2 of these are simply reversals: (1,2,3,4) has the same spiral symmetry axis as the spiral (4,3,2,1). That leaves 12 spirals/Tetrahelix.
For more details on the way 12 Tetrahelix axes pass through a single Tetrahedron, see the next web page.
I find that there is a Clockwise and a Counterclockwise spiral associated with every Tetrahelix.
Note that the spacing between adjacent loops in the spiral is different for the CCW spiral versus the CW spiral.
In both cases, the spirals pass through all the vertices in a Tetrahedron sequentially.
In both cases, the spiral travels a distance along the z-axis by an amonut
But in one case, the spiral travels around the Tetrahelix by an angular amount of
theta = arccos(-2/3) (approximately 131.8103149 degrees)
and in the other case, the spiral travels around the Tetrahelix by an angular amount of
alpha = 360 - arccos(-2/3) (approximately 228.1896851 degrees)
(My notes on this (dated 1997) suggests that I am not the originator of this. Unfortunately, they do not indicate who suggested this originally.)If the tetrahedra used to build the tetrahelix are 10-frequency (have 11 vertices per edge) then the axis of the surrounding tetrahelix cylinder will always pass through the tetrahedra faces at an inner triangular face vertex. The "triangular face coordinate" which the symmetry axis passes through is (7,3).

Click here to see my proof of this.
For a finite length Tetrahelix, all of the Tetrahelix's vertices can be given rational (x, y, z) coordinates. Then by scaling, the coordinates' x, y, z, components can be made to be integers.
I have found that if you allow the vertices to be flexible and allow some of the tetrahedra egdes to expand in length, the tetrahelix can fold up into another (shorter) tetrahelix. When it does, it passes through an Octahedron phase.Here is a sequence of images to help visualize the transformation.First, consider the Tetrahelix to be made up of a number of 3-Tetrahedra units. By folding up each of these units, the Tetrahelix is reduced.We can fold up a 3-Tetra unit as shown in the following figures.

Not that only the C-to-D edge needs to change its length. All other edges of the Tetrahedra remain the same.



At this point, the 3 Tetrahedra are very close to defining an Octahedron. They actually do form an Octahedron as the vertices "A" and "B" are brought closer togther.
When vertices "A" and "B" are brought together, a double Tetrahedron is formed. That is two Tetrahedra face bound togther. (This figure only shows one of the 2 Tetrahedra. The other is hidden behind this one.)

The transformation from the 3 Tetrahedra to the Octahedron Fuller calls the "Richter Transformation". See Color plate 6 in Fuller's book Synergetics. I am not aware that Fuller continued the transformation described here to transform a Tetrahelix.
Joe Matto suggested to me (October, 2004) that 2 Tetrahelix can intersect each other at 90 degrees. If we define "intersect" to mean that the axis of symmetry of 2 Tetrahelix pass through a common Tetrahedron and pass through a common point at 90 degrees, then this statement is not true. The 2 Tetrahelix "intersect" each other at
However, if we define "intersect" to mean that the 2 Tetrahelix pass through a common Tetrahedron and thier symmetry axes pass by each other at 90 degrees, then this is true.
See all the detail on the next Tetrahelix web page.
There are 2 ways to place the end of a Tetrahelix flat on the top of a table such that the Tetrahelix riases above the table. See the calculations here. The angles which the symmetry axis makes with the table top are:
and
References
Here is a list of references. However, I did not use any of these references for my calculations.
- H. S. M. Coxeter, Introduction to Geometry, Wiley: New York, 1969, p. 412.
- Chong Zheng, Roald Hoffman, David R. Nelson, "A Helical Face-Sharing Tetrahedron Chain with Irrational Twist, Stella Quadrangula, and Related Matters", J. Am. Chem. Soc., 112, pp. 3784-3791, 1990.
I have not see the following references. These references are given in the Zheng paper.
- A. H. Boerdjik, Phillips Res. Rep., 7, p. 303, 1952.
- J. D. Bernal, Proc. R. Soc. London Ser. A, 280, p. 299, 1964.
- P. J. Steinhardt, D. R. Nelson, M. Ronchetti, Phys. Rev. Lett., 47, p. 1297, 1981.
- P. J. Steinhardt, D. R. Nelson, M. Ronchetti, Phys. Rev. B, 28, p. 784, 1983.
- D. R. Nelson, Phys. Rev. B, 28, p. 5515, 1983.