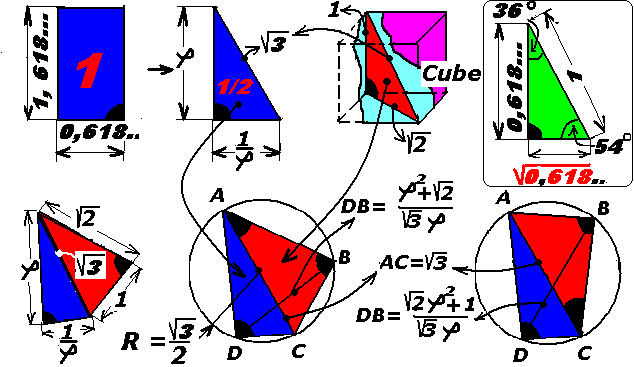|
Article (revised and updated) from collected materials of the 3rd International Research and Application Conference “Tore Technologies” held November 23-24, 2006 at the Irkutsk State Technical University, Russia, pp. 131-143. (Translation from Russian)
TORUS AND SPHERE ARE THE “PARENTS” OF PI (π), PHI AND «7» BEING THE PRINCIPLES OF MATTER STRUCTURING IN NATURE Dr. Valeriy Shikhirin E-mail: info@elastoneering.com, Website: www.elastoneering.com.
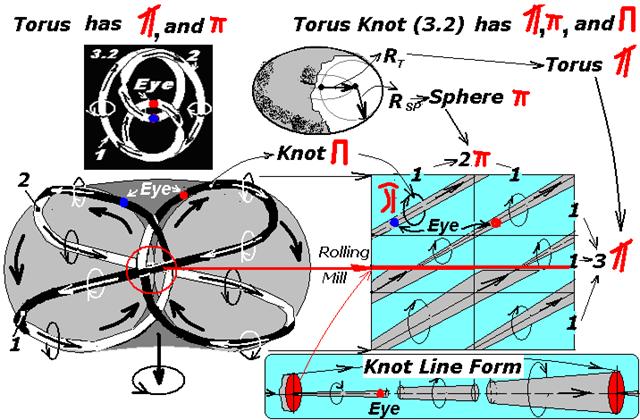
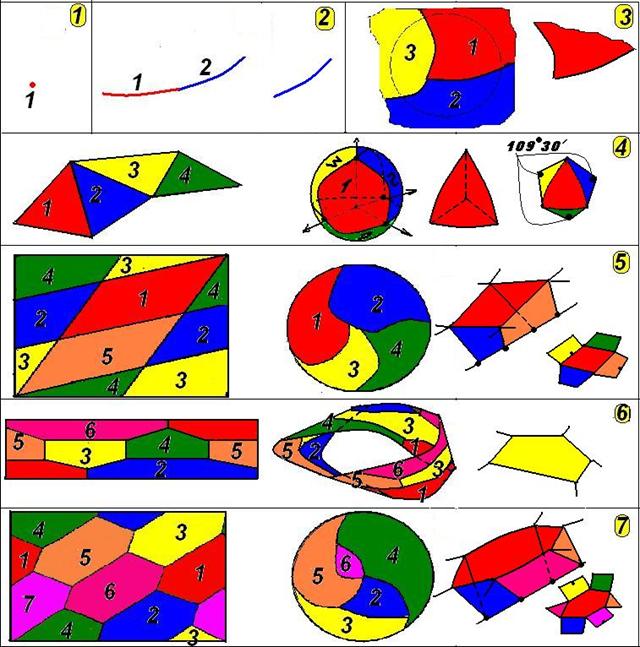
Principles of PI numbers Let us consider “non-flat” versions of PI computation, for example, the relation between volumes, torus and sphere surface areas etc., inscribed into each other; the result of these relations might be integral or fractional PI number (Fig. 1). Fig. 1 «Evolution of spherical π and toric π Here, if: · PI «forms» circle, round, sphere or ball, then this PI is “spherical” π (πSP, Sphere). · PI «forms» tore, and then PI is “toric” π (πT,). In tore shaping process spherical π is the first to act. · PI “forms” active torus knots automatically appearing during tore shaping, and then this PI is “nodal” π (πK, Knot). The number of nodal π is defined by number q – number of coils around tore’s length. · During shaping torus knots spherical and toric PIs are the first and the second to act respectively etc. Numerical meaning of all functional PI is equal to 3,141 592 … The author thinks it absolutely useless to calculate infinitely how many signs follow a comma in a PI. Spherical π We know that the relation of circumference to radius length produces 2π, but this is rather double π than a “single” one; it was obtained experimentally and was observed since great antiquity, at least from the 2nd millennium before our era (Fig.2). Fig. 2 shows the sequence of simultaneous disintegration of a circle inscribed into sphere, “circumference” in a circle and radius in a circle and what such disintegration results in.
This seems to be a unique “direct” computation of double π, in particular: 2π = 2πR/R, and this one is only on a plane. Besides, it is worth considering some other “sphere/circle” relations, for example the ratio of sphere surface area to surface area of a circle inscribed into sphere that produces “number” 4 or 4 “colors” (?) etc. «Defects» and «deficiencies» characterizing careless and neglectful attitude of officials responsible for correct interpretation of PI are described in [7]. Toric π (Fig. 3) 1. If sphere is inscribed into torus or a ball rolls or rests inside hollow ring (closed) with the same radius, then: – Torus surface area and sphere surface area inscribed into torus ratio produces integral “single” π; – Torus surface area and circle surface area inscribed into torus ratio produces 2π, – The relation of surface area to surface area of a flat circular ring with internal radius RRin (Ringinternal) equal to 0 and external radius RRex (Ringexternal) equal to radius inscribed into torus produces 2π, – The relation of torus volume to sphere volume produces 3/2π, or the ratio of three sphere volumes and two torus volumes produces integral π, or torus includes 3/2π of spheres. 2. If tore is inscribed into sphere, then: – Torus surface area and sphere surface area ratio produces ½π or one torus surface area and two spheres surface area ratio; – Torus volume and sphere volume ratio produces 3/8 π or 8 volumes of torus and 3 volumes of sphere ratio. Besides, it is interesting to see other relations between /sphere elements whose formation can be done by pupils in a secondary school. Fig. 3 shows the sequence of simultaneous disintegration of torus inscribed into sphere and sphere inscribed into torus and what is left after such disintegration. |
|
Thus, from above basic relations it follows that: – The relations existing in a sphere inscribed into torus are resulting in degenerated numbers π and π that beside the same irrational numeric meaning characterizing them have neither dimensionality, nor coordinates in space; neither have any ties, no represent a dot etc; – While moving from more complicated figure to less complicated one: → sphere → surface → line segment (also figure, but without surface) → dot (figure without surface and length), the first disappearing figures are multipliers and “flat/spherical”, “volumetric” spherical π, then line segments, but without π. Eventually there remains only one “twisted” toric π intrinsic to tore only, from physical point of view this means that it moves simultaneously rolling along both longitudinal and transverse axes or turning inside out/enveloping (rolling around its transverse circular close axis) and simultaneously twisting/rolling around its polar/longitudinal axis. Then spherical π looks as if it was inscribed into toric π and represents main natural “proportion” to which all-natural structures and processes continuously and inevitably tend. Besides, there exist the relations between PI-figures (sphere) and figures where “direct” PI is not available. – The relations transformed through irrational positive numbers (marked by radical) to spherical π are: · inscribed regular polyhedrons to surface areas and volumes of the spheres they are inscribed into, · inscribed spheres to surface areas and volumes of regular polyhedrons they are inscribed into, · flat rectangle with height h and length equal to diameter length of a cylinder it is inscribed into, · regular prism with height h inscribed into cylinder with height h, · cylinder with height h inscribed into regular prism with height h, · set of 4n facet (with flat base) structural spheres – Shikhirin cells4 (dense pack) inscribed into sphere towards closed line «√1 + π2» etc. – The relations transformed through irrational positive numbers (marked by radical) to toric π are: set of 7np facet (with flat base) structural spheres – Shikhirin cells4 (dense pack) inscribed into torus towards knot’s closed line “7np{nq+ [(nq – 1)/2]}”.
Nodal PI When torus itself turns inside out “active” torus knot (3np; {nq + [(nq – 1)/2]}) also moves [2] and repeats rolling simultaneously along longitudinal and transverse axis. Besides “using” toric and spherical PI, conical closed line of a knot having volume and cyclic channel surface also moves simultaneously along its longitudinal axis (3np + {nq + [(nq – 1)/2]}) times, i.e. it has its own “nodal” PI (Fig. 4). Fig. 4 shows an example of VTortex with torus knot (3.2) and number of PIs involved in it’s functioning. On the left in black visible part of the knot is shown and in white – its invisible part (behind torus).
On the right there is a swelling thread of a knot (law of swelling) [8], whose minimum thickness is formed after super cold cross rolling and maximum thickness – before. It should be kept in mind that torus knot (3np + {nq + [(nq – 1)/2]}) is energy and information characteristic of VTortex, which means that PI is involved in the process of its shaping and filling with energy and information. Thus, VTortex has five (!) functional PIs – «PI5» operating in a 3D space in the following combination: – 1st (spherical) and 2nd (toric) are “responsible” for torus SHAPE, – 3rd (3np spherical), 4th{nq + [(nq – 1)/2]} (toric) and 5th (nodal) are responsible for ENERGY and INFORMATION. This is a torus knot (3np + {nq + [(nq – 1)/2]}) or energy and information Shikhirin’s soliton [2.5].
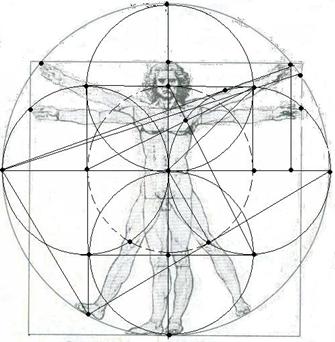
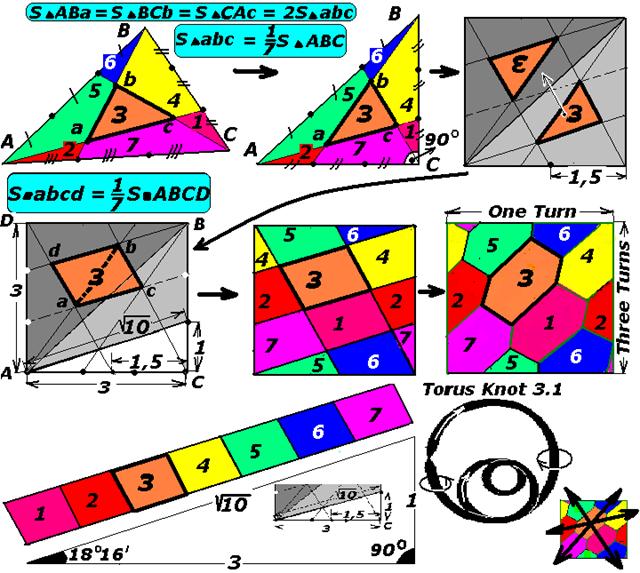
Principals of Golden ratio Let us analyze sphere inscribed into torus (Fig. 5). A reader himself can prove that ∆Ot P2 OT and ∆OT P2 Osp, ∆Ot С2 OT and ∆OT С2 Osp and ∆Ot С1 OT и ∆OT С1 Osp are equal to each other. Let us analyze triangle ∆Ot P2 Osp “single” area comprised of ∆Ot P2 OT and ∆OT P2 Osp with common side P2 Osp equal to √2. There are at least two algorithms allowing formation of “golden ratio” by this triangle: 1. The sum of free sides ∆Ot P2 OT and ∆OT P2 Osp ratio is equal to “golden ratio”, i.e.: (P2Ot + OtOT) / (P2Osp + OspOT) = [(√5 + 1) / (1 + 1)] = [(√5 + 1)/2] = 1,618… = φ, and the difference of free sides ∆Ot P2 OT and ∆OT P2 Osp ratio is equal to inverse value of “golden ratio”, i.e.: (P2 Ot – Ot OT)/(P2 Osp + Osp OT) = P2 C1/(P2 Osp + Osp OT) = [(√5 – 1)/(1 + 1)] = [(√5 – 1)/2] = 0,618… = 1/φ. 2. The relation of hypotenuse length and small leg sum to great leg ∆Ot P2 Osp is equal to “golden ratio”, i.e.: (P2Ot + P2Osp)/OspOt = [(√5 + 1)/2] = 1,618… = φ, and relation of hypotenuse length and small leg difference to great leg ∆Ot P2 Osp is equal to inverse value of “golden ratio”, i.e.: (P2Ot – P2Osp)/OspOt = [(√5 – 1)/2] = 0,618… = 1/φ. Fig. 5 shows “appearance/birth” of “golden ratio” with the help of its “parents”: sphere inscribed into torus. Thus, torus and sphere inscribed into torus are “parents” of interrelated “PI numbers” and “ancestors” of φ. This is “Gold Pair” or “Shikhirin’s Pair”. Right-angled triangle ∆OtР2Osp is called “Goldest Triangle” or “Shikhirin’s Triangle” consisting of two triangles with equal areas. Moreover: 1. The product of “golden ratio” φ and its inverse value 1/φ, namely: [(√5 + 1)/2] х [(√5 – 1)/2] = 1, 618…х 0,618… = φ x 1/φ = 1, i.e. the area of rectangle with sides φ and 1/φ, is equal to “One”; physically this is rather “one area” or one “color” than just a unit not tied to anything. The area of goldest triangle is also equal to “one”.2. When sphere inscribed into torus and torus interact (Fig. 6) a set of triangles is formed having definite physical destination – formation of: – “numbers” √2, √3, √5, √7 and the composition thereof, – numbers 1, 2, 3 and 4, – proper and improper fractions, – «golden ration» and its combination etc. – “number”√10 and a line of torus knot (3.1) along which seven “colors’ and dense pack of Shikhirin cells7 are formed (see also Fig. 11) etc. Fig. 6. A set of torus triangles formed when sphere is inscribed into torus.
The author made a simple experiment: the picture “Virtrunian Man”, 1490, painted by Leonardo Da Vinci was laid on “goldest pair” (Fig. 5). The author claims that “ToruSpherical Man” is a “medium” for all “principles”: various – purpose PIs; golden ratio; roots of 2, 3, 5, 7 and the combination thereof; “numbers” 1, 2, 3, 4, 7 etc.; proper and improper fractions; geometric parameters of Plato and Archimedean solids etc. Fig.7. “ToruSpherical Man”, “Man is a Measure of All Things”, Protagora of Abdera. This provides to enthusiasts/amateurs and practical researches in any field of Science enormous capabilities to “play” with “gold pair” by putting it on any natural object or process in micro-, macro and/or mega worlds or their elements. The author is confident that such games will reveal the peculiarities of matter structuring in the Universe and will give answers to such phenomena that are unknown to Science and do not follow the laws of physics; this will put an end to such phase as “generally accepted” and those who elaborated it and widely uses.
3. Some other features of golden ration φ (Fig. 7) noticed by the author: – diagonal of goldest rectangle or hypotenuse of goldest triangle is equal to √3; this is a formation of “number’’ √3, – diagonal of cube face is equal to √2; this is a formation of “number” √2 like in two torus triangles, – diagonal of cube face is equal to √3 as well as diagonal of goldest rectangle, – convex quadrangle comprised of goldest triangle and triangle obtained by dividing diagonal cube face into two equal parts connected over common diagonal (equal to √3). Such rectangle is inscribed into circle with radius √3/2 and possesses all properties of rectangle inscribed into circle of rectangle, for example according to Ptolemy Theorem. – sphere and torus surfaces area and volumes with radiuses √3π/2 are equal to 3π square units and √3π/2 cubic units and 3π2 square units and 3√3π2/4 cubic units respectively. – hypotenuse of right-angled square with legs 1/φ and √1/φ is equal to “1”. Fig. 8. “Goldest” rectangle and “Cube”
In next articles the author will describe forming technology (structuring) existing in Nature for regular polyhedrons, Shikhirin cells4,6,7, dense pack comprised of them, already produced or being produced in a time from fluid medium etc., particularly their “basic” elements [5]: – regular dodecahedrons, icosahedrons and their derivatives – Foam4, – irregular distorted (oblong and/or flattened) dodecahedrons, icosahedrons and their derivatives – Band4, – regular Shikhirin cells4,6,7 and their derivatives – Foam7, – irregular distorted (oblong and/or flattened) Shikhirin cells4,6,7 and their derivatives – Band7 etc.
The author’s digression. 1. It is known that Plato’s bodies including dodecahedrons and icosahedrons have three companion spheres: – the 1st internal sphere is inscribed into polyhedron, touches its facets and “burst open” its volume, – the 2nd middle sphere touches its edges and “holds/keeps” its volume, – the 3rd external sphere is inscribed around polyhedron, touches its crowns and “encloses” its volume. Similar to dodecahedrons and their modifications the set of seven polyhedrons7, distorted Shikhirin cells7 forming tore, also has three companion tores: – the 1st internal tore is inscribed into a set of seven polyhedrons7, touches the facets of their base – honeycombs and “burst open” its volume, – the 2nd middle tore touches the edges of base-honeycombs and “holds/keeps” its volume, – the 3rd external tore is inscribed around the set of seven polyhedrons7, touches the crowns of base- honeycombs and “encloses” its volume. Let us call this process as respective polyhedrons sphere – and tore accompaniment or accompaniment of respective sphere and tore polyhedrons. 2. “Dodecahedron and its modification” Concept. Symbol of polyhedron is (А{В}), where А – number of facets, В – number of angles in a polyhedron (В-angle): – Dodecahedron – 12{5}, – Icosahedron – 20{3}, – b- tetrakaidecahedron (Beta-tetrakaidecahedron) – 4{6} + 8{5} + 2{4} – Truncated Icosahedron – 20{6} + 12{5} etc. Dodecahedrons and their modifications (not only) during their deformation, stretching and rotation are topologically unchangeable; it means that their qualitative information (number of facets, crowns, edges etc.) also is not subjected to changes. The end of digression.
Principles of numbers 1, 2, 3, 4, 5, 6 and 7 In [2] it is shown that “four” (sphere), ‘six” (Mobius band) and ‘seven” (tore) “colors” are the base of Shikhirin cells4,6,7 , including tetrahedrons, “flat” pentahedrons and heptahedrons. In [5] it is shown that sphere, Mobius band and tore consist of dense pack (minimum set), four Shikhirin cells4, five Shikhirin cells5 and seven Shikhirin cells7 (Shikhirin cells4,5,7) that represent sphere shaped shells filled with flowing medium at excessive pressure with a field (charge) of pressure in each shell having maximum pressure charge concentration distributed in non-linear, specific way in each type of the cell.
Similar to previous studies on “colored” structuring, in particular “colors” having common bodies and located on the following objects – forms representing missing “principles” of numbers 1,2,3, and 5 (Fig. 8): – «1» – one “color” – on/in a point, – «2» – two “colors” – on a line segment, – «3» – three “colors” – on a surface, – «4» – four “colors” on the surface of volumetric figure – sphere, – «5» – five “dirty” “colors” on a volumetric figure – tore, – «6» – six “colors” on the surface of volumetric figure – Mobius band, – «7» – seven “colors” on the surface of volumetric figure – tore Fig. 9 «Colored» structuring of various figures
Let us examine the most “popular” numbers 4 and 7.
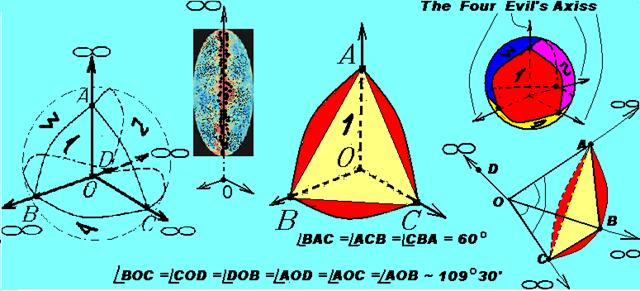
Principles of number 4 Sphere consists of dense pack of 4 Shikhirin cells4 – four trihedral angles (4 angled regular pyramids) АВСО, ABDO, DACO and DBCO whose edges represent radiuses of sphere, О – their crowns and flat angles at the crowns are ≈ 1090301. The cut of 3-facet angles by a plane not crossing their crown represents equilateral triangle. Sphere with infinite radius (Universe) (Fig.9) consists of “dense pack”- four Shikhirin cells4 with 4 “Axes of Evil”, infinite edges-radiuses (infinite 3-facet angles – 3-facet funnels) coming from centre О, structural centre of Universe being the start of Universe structuring – «Evil’s Center». Data obtained with testing probe НАСА WMAR and processed according to criteria of “fluctuations of microwave radiation temperature on coelosphere” [9] showed ordered distribution of “cold” and “warm” areas: concentration of galaxies along the axis – «The Axis of Evil». Fig. 10. Universe Structure: four Shikhirin cells4 with infinite edges – four infinite 3-facet angles filled with dense pack of dodecahedrons or their combinations. The picture is turned to 900 and demonstrates one “the axes of evil” ОА.
Testing probe has “seen” only part of one of 4 infinite “axes of evil” – Plato channels resting on “the Axis of Evil” or one of four facets half face. And “Axes of Evil” are actually four “edges” of 4 facets-films of densely packed with 4 infinite 3-facet angles structural spheres-bubbles (Shikhirin cells4) . Then four infinite 3-facet angles are filled with dodecahedrons or their modifications, for example tetrakaidecahedron, which, in their turn, are combined into clusters, mega clusters, mega-megaclusters etc; their edges, including infinite 3-facet angles, “repeat” the edges of boundary dodecahedrons, i.e. represent broken angled surface. The principles of their combination correspond to the principle of keeping the strength of Universe structure while its constituents increase due to their physical characteristics, i.e. with account for specific features of “scale effect” (see below in the text).
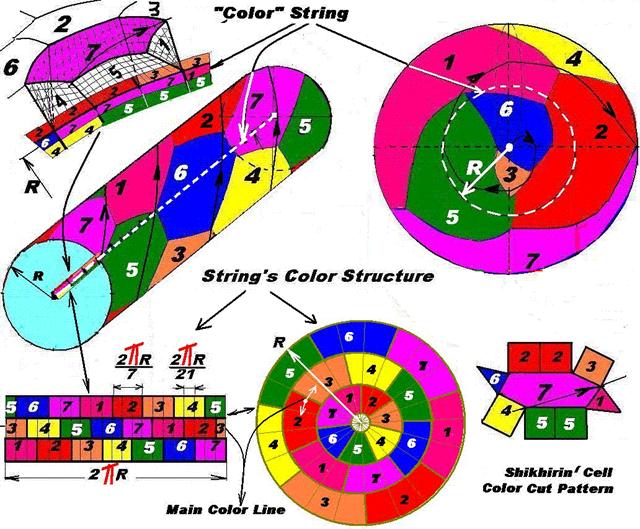
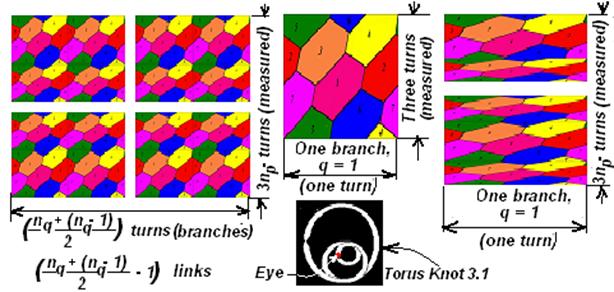
“Principles” of Number «7» Everything is a number and everything derived from number sevenPyphagor – PythagorasThe author uses “topological” terminology because, for example, longitude in topology and geodesy has different meaning. Let us describe in details functional features of VTortexs partially described in [5]. VTortexTM – is self- sustained toroidal, eversible/enveloping structure being at the same time the source of energy and information. For example, smoke ring of a smoker exists only several seconds, tornado – several days and Galaxy – tens and hundreds of thousands years measured by Earth measurements. The life of any Humanity on any planet adapted by them (or their ancestors) for life is limited by 10 thousand years because of natural cooling on Earth [8] caused by the movement of Solar system where the Galaxy is turning inside out of its life belt towards super cold zone. VTortex – is a smart 3np– dimensional {nq + [(nq – 1)/2]} branch toroidal soliton (Shirhirin’s soliton) (Fig.8) made of dense pack {7np{nq + [(nq – 1)/2]} of structural spheres/bubbles – Shikhirin cells7; meantime the outer surface is reinforced with torus knot (3np; {nq +[(nq – 1)/2]}) with parameters (p, q) [10], where: · p = 3pnp – number of turns around meridian VTortex (polar/longitudinal axis), · 3p – sequence of numbers 3, 6, 9, 12 … consisting of 3 and numbers multiple to 3, and np – numbers of natural scale, several hundreds/thousands, · q = {nq + [(nq – 1)/2]} – number of turns around longitude, i.e. 1,2,4,5,7,8,10,… consisting of natural numbers except 3 and numbers multiple to 3, where nq are numbers of natural scale; the operation [Х] is the operation of integer part derivation (integer division) The basic types of Shikhirin’s soliton are: – non-working/static/non-eversible smart toroidal 3-dimensional single branch “soliton” (boublic) made of dense pack of 7 structural spheres/bubbles – Shikhirin cells7 whose outer surface is reinforced by knot 3.1 (Fig.8, 9). – continuous spiral line of knot 3.1 embraces torus surface three times around meridian and once around its longitude. Along this line there are 7 color zones/ rectangles having common borders [11]. On a plane (not on torus involute) [12]: – 7 color zones/ rectangles are transformed to 7 color zones/ honeycomb cells having common borders, – found two directions for the formation of 7 color zones – cells. For toroidal surface the author developed the following: – 7 color zones/rectangles are transformed to 7, then to 7 np {nq + [(nq – 1)/2]} color zones/honeycomb cells, having common borders, – found the third direction in the formation of 7 color zones – cells [5], – 7np color zones/honeycomb cells with common borders cover toroidal surface by three ways, – 7np color zones/honeycomb cells are the bases of dense pack of 7np structural spheres/bubbles – Shikhirin cells7 (Fig. 8), – when p and q parameters in torus knot (3np; {nq + [(nq – 1)/2]}) change their position, i.e. ({nq + [(nq – 1)/2], 3np }), there also remain 7np color zones/honeycomb cells having common borders covering toroidal surface. For example torus knot (3,1) is transformed into (1,3), knot (3.2) into “Trefoil Knot” (2,3) [13] and knot (3,5) into knot (5,3). In this case 7 “colors” are formed in different direction and it can be seen that tore surface involute turns 900. This means that seven “colors” are formed in three directions relative to the tore knots line: (3.1), (1.3) and (2.3) (Fig. 10). – torus string is not only the contracting center; it is structured in a special way to become information “principle” for torus generation in the form of energy and information soliton. – on all “cut out” patterns or torus involutes there is shown a knot line (3np, {nq + [(nq – 1)/2]} with a peculiar feature – Links in the central part of torus, whose number is equal to ({nq + [(nq – 1)/2]} – 1). From physical point of view these links play the following role: – Keep VTortex from its transformation from close to open torus and consequently from its further disintegration. The analogy is the smoker’s ring, whose outside and internal diameters increase within some time, which eventually leads to smoke torus break up (disintegration). – They are cinematically non-detachable rollers of super cold helical rolling, for example planets and hailstones. Fig. 10. Knot 3.1 – theoretical, typical smart three-dimensional toroidal soliton, whose surface is, covered with 7 colors zones/honeycomb cells having common boundaries. The picture of tore knots is taken from [10]. In Nature it works for a short time because it does not have counterbalance, for example 2nd branch or “works” in forced rotating fluid medium (in a glass). The examples of theoretical and natural Shikhirin’s solitons are shown on Figs. 11, 12. Fig. 11 shows the surfaces involutes (cut out patterns): On the left there is smart 3np – dimensional {nq + [(nq – 1)/2]} branch toroidal soliton (Shikhirin’s soliton), in the middle there is non-working/static/non-eversible smart 3-dimensional single branch toroidal soliton (boublic or wheel chamber) and its “eye, on the right there is smart 3np – dimensional single branch toroidal soliton. Fig.12 shows surfaces involutes (cut out patterns):
On the left: galaxy – smart 3np -dimensional 2 branch toroidal soliton, On the right: tornado – smart 3np -dimensional 5 branch toroidal soliton. In both solitons there is marked central part where majority of involutes are spanned; they perform the function of rollers in natural helical rolling mill of planets and hailstones respectively.
Natural technology of generating seven zones – honeycomb cells on toroidal surface or its structuring. There is a known a task to divide any triangle into seven parts with straight lines ”seven-component triangle” (Fig.11, on the left, top) and to provide adequate proof [14, 15]. Straight lines are drawn from vertex of triangle consecutively, either clockwise or counter-clockwise to the points on opposite sides of triangle; these points divide the sides in 1/3 to 2/3 ratio. The area of triangle obtained at concurrence of straight lines comprises 1/7 of entire triangle area. The author supplemented this know task as follows (Fig. 11): – The same operations were applied to 45 º right triangle, then the author comprised a square of two 45 º right triangles: close torus involute. – Then after some geometric transformations he showed that a square is split into seven identical parallelograms. – Then he transformed parallelograms to elongated zones-cells. In the process of torus generation zones/honeycomb cells are transformed from flat involute to the bases of dense pack figures of Shikhirin cells and the line along which dense pack is generated is a torus knot (3.1). Seven colors can be generated in three directions. Fig. 13 Technology of generating seven zones/honeycomb cells on a toroidal surface.
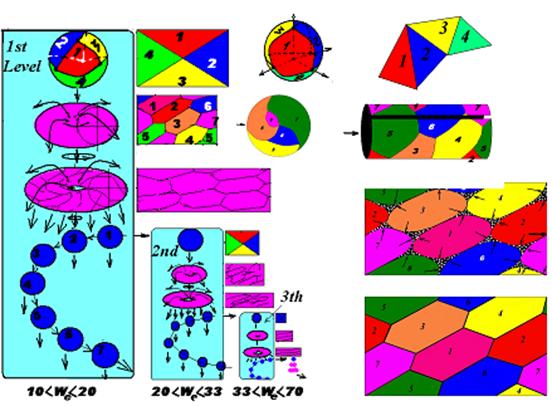
From generally known experiment describing successive behavior of ink drop in water, for example in [16] it follows that ink vortex ring is generated in water, then after a time it splits into several new vortex rings of smaller size, which in their turn also split etc. Direct proof of seven-component torus is the research as in [17] proving that at all levels of “volumetric graph” consisting of vortex rings the number of vortex rings obtained by splitting previous vortex ring is equal to 7. The real (topological) process of vortex ring generation from a drop looks as follows (Fig. 14): Fig.14. On the left natural transformation of falling or blown liquid drop is shown: drop (ball) – closed torus – open torus (ring) – 7 drops (balls) etc. On the right involute of sphere and torus with “four colors” and “seven colors” is shown respectively.
The volume of 4 color sphere is equal to the volume of 7 color torus and the radius of torus after its transformation from sphere (liquid ball) will have the following relation: Rt = Rsp3√2π/3. The real picture of a drop disintegration (Fig. 14) by «accompanying» spheres and tores looks as follows: – The 1st spherical drop (first level) is distorted dodecahedral or its modification inscribed into “middle” sphere touching its edges, – The second and the next drops (second level) generated from tore disintegration are distorted Shikhirin cells7. The set made of seven Shikhirin cells7 is inscribed into “middle” tore touching the edges of base- honeycombs.
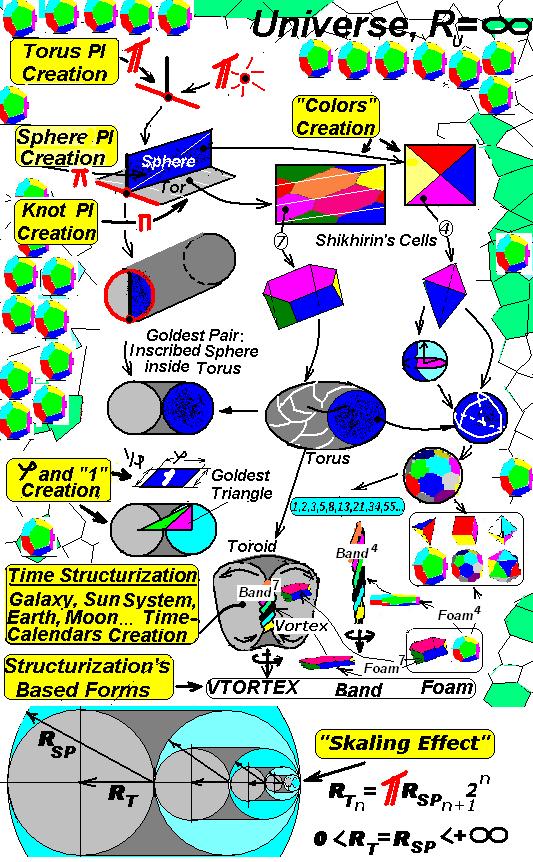
Drop → ring without a “hole”, closed eversible torus → ring with a hole, open eversible torus/ring. Moreover: – np, besides being the numbers of natural scale, this is also a number of levels/cycles of vortex ring division, – 1st level is the first vortex ring, – totally there will be 7np rings obtained as the result of “drop” division excluding the first level ring. The number of levels means the optimal number of structural bubbles – Shikhirin cells built in torus moving in particular fluid medium. The features of vortex liquid or/and gas ring in liquid and or/and gas medium divisions are: – Appearance of 7 bulges – Shikhirin cells7, – Bulges appear one by one from “top to bottom” along continuous helical line of a knot (3.1), – New “drops” appear from bulges also successively, – Each “drop” is transformed to vortex ring etc. [7 (n -1)] times in total, – Drop division rate depends on its diameter, liquid or gas surface tension, speed and density of blown liquid or gas [18]. For example, if gas pressure РG (Gauze) in frontal point of a drop where it has the largest value and equal to velocity head ρu2/2, the flow of flowing gas is completely hampered. If according to Laplace formula the pressure of surface tension PL (Liquid) for liquid ball is PL=4σ/а, then the relation PG/PL is deformation and splitting complex or criteria of falling or gas blown liquid drop: Weber number (We): PG/PL ≈ We = ρu2 а/σ. At 10<We<20 falling or gas blown drop will be transformed to vortex ring and divided into 7 drops → rings etc. At 20 <We < 33 and 33 <We < 70 falling or gas blown drop will be transformed to vortex ring and divided sequentially (as if it were simultaneous) into 7 → 7( np-1) → 7( np-2) → 7( np-3)… drops → rings … It is necessary to pay attention to the following most important feature of drop and torus Levitation or Gravitation –Vtortex: torus “flies” or “falls” quicker! Why? The explanation is: in front of tore enveloping end, an implosive centrifugal outflow, a discharged P– zone/void/cone (Low Pressure Cone) is formed, meantime in front of its eversible end, an implosive centrifugal source, charged P+zone/void/cone (High Pressure Cone) is formed. This means that torus retracts itself to discharged zone thus increasing its translation speed [2] and “leaving behind” a drop. Torus-Vtortex is becoming a driver of unsupported motion. Fig. 15. Energy and information “principles” of Nature or “Formation” and Hierarchy of relations (Harmony) of spherical, toric, nodal PI and golden ratio φ, regular polyhedron, Fibonacci numbers etc., as well as basic forms of fluid medium structuring [5], calendars of Galaxy, Solar system, Earth [8] etc.
The author made an attempt to summarize “principles” of matter structuring available in Nature in a Table that will be constantly improved and supplemented (Fig. 13). The Table is open for all volunteers – patricians who are eager to make it as “Energy and Information Principles of Nature”.
Scaling Effect
It is known from the analysis of disasters that the larger is an object (ship, bridge, multi-story building etc.), the more fragile becomes the material, which leads to quick destruction of the object and disastrous effects. In Nature there exist really huge objects, for example planets, solar systems, Galaxies etc. having definite physical parameters that are automatically controlled thus preventing their damage for a pretty long time. However, when certain standard proportions are violated this immediately causes damage of natural elements, for example, break of planets’ crust, “blast” of Galaxies, tornado dissipation etc. The author believes that regardless the objects volume the ratio of the volume of sphere inscribed into torus with equal radiuses and then torus with ½ radius inscribed into this sphere etc. should according to the principle of “matreshka” correspond to the ratio RTn = RSPn+1π2n, where Tn is torus with π2n more radius than the radius of sphere into which this torus is inscribed (Fig. 13, in the bottom). This is a stability condition for natural or man-made objects preventing their destruction. Or RSPn+1/RTn=1/π2n The sum of geometric series is 1/π (1 + 1/2 + 1/22 + 1/23 +…+ 1/2n) < 2
Conclusions 1. The ratio of close torus and inscribed sphere areas is prime and main natural ratio, in particular: “PI-Goldest Ratio” or “Shikhirin’s Ratio” being the source for spherical π and toric π, and consequently the appearance of golden ratio φ. This means that toric π and spherical π are primordial to φ. 2. The area of a rectangle with sides φ and 1/φ is equal to “One” whose physical meaning is “single area”. “One” is a product of “golden ratio” and its inverse value, i.e. 1 (quadric units) = 1, 618…х 1/1,618… = 1, 618…х 0,618…. This means that all numbers are areas equal to their numeric values (in quadric units). 3. The volume of parallelepiped, “goldest brick”, with sides φ, 1/φ and spherical π. is equal to 1, 618…х 0,618…х π. 4. “Goldest” sphere is a sphere having: – radius equal to 3√3/4, – surface area equal to 4πRsp2 = 4π(3√3/4)2, – volume equal to π (cubic units). 5. “Goldest” torus (close torus) is a torus having: – radiuses equal to radius of “goldest” sphere 3√3/4 inscribed into this, – surface area equal to 4ππRt2 = 4ππ(3√3/4)2 (π-quadric units), – volume equal to 3/2ππ (π-cubic units). 4. “Direct” golden ratio φ and/or its elements are available only in “noncircular” (without PI) linear, area and volumetric bodies, for example in Plato and Archimedean bodies, their modifications or in a package comprising them, inscribed into sphere or described by sphere, i.e. it is responsible only for “faceted” linear, flat and volumetric bodies. The examples in Nature are: – In foam consisting of dense pack of dodecahedrons, icosahedrons etc. with golden section; spherical π is directly present only in inscribed or described spherical shell enclosing or bursting out foam volume. Linear sizes of polyhedron elements expressed through angular parameters, i.e. through π are not “direct action” of π. The process starts with the increase of spheres-bubbles sizes, which happens because their shells are burst out by fluid/working medium at excess pressure inside this shell. There is π-generation process where “spherical” π appears. Then spheres-bubbles tend to be shaped into regular polyhedrons. Then the so-called de-πization take place and “spherical” π disappears. – In foam of Shikhirin cells7 dense pack where directly “golden” ratio is not present, toric π is directly present in toroidal shell, enclosing foam volume; both toric π and spherical π are directly present in Shikhirin cells7. 5. According to natural hierarchical level Golden ratio φ is a special case or derivative of simultaneously interacting spherical π and toric π in a sphere inscribed into torus. 6. There is “direct” “golden section” neither in torus, nor in sphere, nor in Mobius band and projection plane, nor in their elements – Shikhirin cells4,6,7 comprising their volume. 7. Spherical π and toric π existing in unified formula simultaneously with φ, for example in the calculation of elements of flat “golden”, “sacred” and other triangles, are not results of their direct linkage, this means that these parameters are only expressed through them and are not available in real parameters of natural “golden” objects. 8. Physical interrelations existing between number е, spherical π, toric π and “golden” ratio φ being energy and information principles of Nature will be described in the next author’s generations. 9. In the interaction of sphere inscribed into torus (Fig. 6) a set of torus triangles is generated with definite physical destination: formation of “numbers” √2, 2 , √3, √5, √10 of golden ratio and its derivatives, seven “colors” and dense pack of Shikhirin cells7 – torus etc. 10. Formation through cube: – “numbers” √2: diagonal of cube facet is equal to √2, – “numbers” √3: diagonal of cube facet is equal to √3 as well as diagonal of goldest rectangle is equal to √3. 11. Hypotenuse of right-angled triangle with legs 1/φ and √1/φ is equal to “1” etc. 12. When torus is formed from its flat involute, zones-cells are transformed into dense pack bases of seven Shikhirin cells7 and a line along which dense pack is formed represents torus knot (3.1). Seven “colors” are generated in three directions. 13. When parameters p and q in torus knot (3np; {nq + [(nq – 1)/2]}) change their places, i.e. ({nq + [(nq – 1)/2], 3np}), 7np color zones/ cells having common boundaries covering toroidal surface also remain. In this case 7 “colors” are formed in a different direction, whereas visually torus surface involute turns to 900. 14. “Working’ torus-VTortex apart from spherical and toric PI has “nodal PI”. Totally torus-VTortex has five (!) functional PIs – “PI5” operating in three dimensional spaces in the following combination: 1st (spherical) and 2nd (toric) are “responsible” for torus SHAPE, – 3rd (3np spherical), 4th{nq + [(nq – 1)/2]} (toric) and 5th (nodal) are responsible for ENERGY and INFORMATION. This is torus knot (3np + {nq + [(nq – 1)/2]}) or energy and information Shikhirin’s soliton 15. Scaling effect – regardless objects volume the ratio of the volume of sphere inscribed into torus with equal radiuses and then torus with ½ radius inscribed into other sphere etc. should according to the principle of “matreshka” correspond to the ratio RTn = RSPn+1π2n, where Tn is torus with π2n more radius than the radius of sphere into which this torus is inscribed.
Literature 1. A. Stakhov, A. Sluchenkova, I. Sherbakov. Da Vinchi Code and Fibonacci Rows. “Piter”, St. Petersburg, 2006. 2. V.N. Shikhirin. VTortexТМ is the Highest Form of Fluid Medium Structuring in Nature. Article in the Collection of the 3rd International scientific and practical conference “Tore Technologies”, November 23-24, 2006, Irkutsk State Technical University, p. 158-179 www.evgars.com/vtortex_e.htm. 3. B.S. Gorobets. World Constants π and ℮ in Main Laws of Physics and Physiology. Science and Life or http:// www.arbuz.uz/t_e_pi.html 4. Josev Hasslberger. Tetra Space Co-ordinates, A tetrahedron-based system of space co-ordinates, Rome, Italy, 3 February 1996 or http://www.hasslberger.com/phy/phy_6.htm 5. V.N. Shikhirin. Prospects of Development of Tore Technologies, Elastic Engineering and “Wonders” Created by them in Nature. Article in the Collection of the 2nd International scientific and practical conference “Tore Technologies”, September 21-24, 2005, Irkutsk State Technical University, plenary report, p. 3-41. www.evgars.com/tore_technology.htm 6. V.N. Shikhirin. Analysis of the Capabilities of Using Mathematical Methods for Die Molds Distribution in Casthouse of Izhevsk Machine Works. Diploma project. Izhevsk mechanical institute, 1971 7. Alexey Arsentiev. Artifact of PI Number as an Error of Collective Perception. http:// www.arbuz.uz/t_pi.html 8. V.N. Shikhirin. VTortex- Galaxy as Structurizer of Star Systems, Time and the Cause of Climate Change on Earth. Article in the Collection of the 3rd International scientific and practical conference “Tore Technologies”, November 23-24, 2006, Irkutsk State Technical University, p. 143-158, www.evgars.com/climatе_e.htm 9. Kate Land and Joao Magueijo. The axis of evil, ArXiv.astr-ph/0502237 v2, 22Feb 200532 10. www.library.wolfram.com/webMathematica/Mathematics/Knots.jsp 11. Martin Gardner. Mathematical Puzzles and Entertainment (The Problem of Four Colors), Moscow, Mir Publishers, 1999 12. Stan Tenen. Hex-Pattern 7-color map, defining a 2- 1984 http://www.meru.org/Posters/hex.html 13. Knots in the Seven Color Map by Lois H. Kauffman, http://www.math.uic.edu/~kauffman/ 14. G. Shteinhaus. Mathematical kaleidoscope. Authorized translation from Polish. State Publishing House for technical and theoretical literature, Moscow-Leningrad, 1949, p. 9. 15. D. Goryachev, A. Voronets. Tasks, questions and sophisms. For mathematic fanciers. NITS “Regular and chaotic dynamics”, Moscow-Izhevsk, 2000. 16. S. Shabanov, V. Shubin. About Vortex Rings. From Home Laboratory Experiments (Helmholtz experiments), Moscow, Science, 1980. Library series “Kvant”, issue 4, p. 18-28 17. Danial Winter. 7 Arrows of the Heart and 7 Colors of the Rainbow, from the Hydrodynamics of the Perfect Inc ‘Drop’? www.soulinvitation.com or www.spirals.eternite.com 18. M.S. Volsky. Unusual Life of Usual Drop. Nauka and Progress. “Znanye”, Moscow, 1986 19. V.N. Shikhirin. Tore Technologies – the Basis of Elastic Engineering. Article in the Collection of the 1st International scientific and practical conference “Tore Technologies”, June 30 – July 2, 2004, Irkutsk State Technical University, plenary report, p. 22-48. www.evgars.com/elastic_mechanik.htm 20. V.N. Shikhirin. Vehicles’ toroidal drivers. Article in the Collection of the 2nd International scientific and practical conference “Tore Technologies”, September 21-21, 2005, Irkutsk State Technical University, plenary report, p. 79-99. www.evgars.com/tore_transport.htm 21. V.N. Shikhirin, V.F. Ionova, O.V. Shalnev, V.I. Kotlyarenko. Elastic mechanisms and structures. Monograph. Scientific edition of Irkutsk State Technical University, 2006. 22. V. Shikhirin. Natural “Elements” of Information and Energy as the Basis for XXI Century Engineering. Structurization InfEnergy. Proceedings of the 4-th Research & Engineering Conference “Machine Building”. Science, Education and Production Integration, May 2007, Izhevsk State Technical University www.evgars.com/infenergy1_e.htm 23. V. Shikhirin. Natural “Elements” of Information and Energy as the Basis for XXI Century Engineering. Natural and Mechanical Implementation. Proceedings of the 4-th Research & Engineering Conference “Machine Building”. Science, Education and Production Integration, May 2007, Izhevsk State Technical University www.evgars.com/infenergy2_e.htm
|
|
© 2015 Freely quoted with reference to the website of the author Свободноцитируемый, со ссылкой на веб-сайт автора |