047 EU Meetup August 28rd, 2018

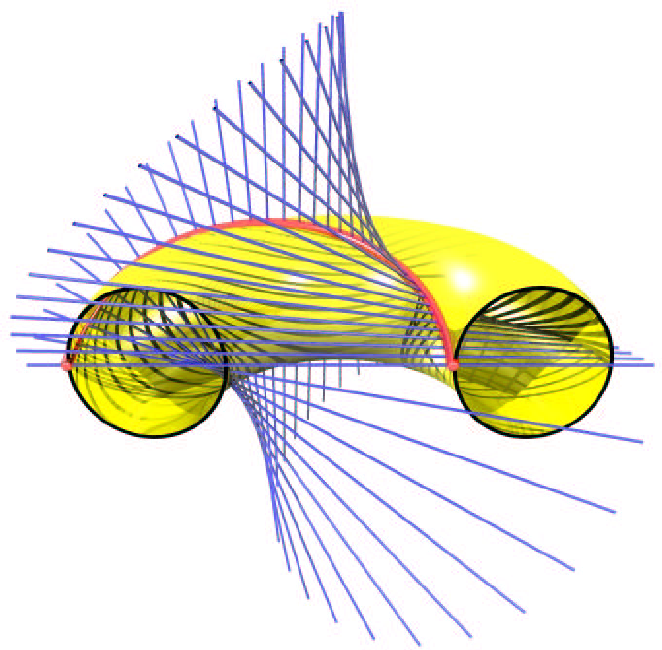
… Odehnal: Common Normals of Two Tori 61 The generators of the quartic ruled surface Φ defined by (19) carring the continuum of common normals of T 1 and T 2 meet the spine curves s 1 and s 2 orthogonally. This is equivalent to s 1 − s 2 , s ̇ 1 − s 1 − s 2 , s ̇ 2 = 0. Integration yields s 1 − s 2 , s 1 − s 2 = const . and consequently on each common normal the two spine curves enclose a segment of the same length. Thus we have Thus s 2 is a Villarceau-circle of a torus T 1 with spine curve s 1 . For Villarceau sections and generalizations the reader may be referred to [1, 11, 14]. On the other hand we can shrink T 1 such that it degenerates to s 1 and simultaneously we can blow up T 2 such that s 1 becomes one of its Villarceau-circles. Both cases can be seen as borderline cases of tori with infintely many common normals. This is illustrated in Fig. 7. The right choice of radii of meridian curves of T 1 and T 2 , respectively, leads to tori in line contact. In this case the meridian radii r 1 and r 2 sum up to 2 d . Since the curve of intersection of two tori is of degree eight and both surfaces share the absolute conic 3 the curve of contact is of degree four. In general it is not a circle with multiplicity two since Φ given by (19) contains only the two circles s 1 and s 2 , respectively.