We see at school that when we squared the number √2 (that is, when we multiply √2 by itself), we get 2. For a long time mathematicians wondered if numbers like √2 really exist, but they didn’t find the answer . What have you done? They invented an answer that is not quite an answer and moved on, happily doing math.
{1} / A matter of defining well
The teacher (let’s call him Moses ) enters the class, puts a big roll of paper on the table, takes a roll of masking tape from the pocket of his white coat and also puts it on the table, wishes the class a good day, and finally draws a simple formula on the blackboard:
x 2 = 2
He turns to the class and asks:
“Guys, how much is x worth ?”
One of the students answers, half in doubt:
“Root of two.”
“It’s what I expected to hear,” says Moses. He turns to the board again and draws the root symbol of two: √2. “How do you know this number exists?”
Several students give some version of the most common answers: it exists because the teacher said it exists; it exists because the calculator says it exists; it exists because it is precisely the number that, when multiplied by itself, gives 2; exists because, if not, how to solve the blackboard equation?
“Right. The symbol √2 denotes a positive number x which, when multiplied by itself, results in 2. Please don’t forget: –√2 is also a root of the equation x 2 = 2, because (–√2) 2 also is equal to 2. But in today’s discussion, for simplicity, let’s talk about non-negative numbers. ”
Draw on the board what you just said, so that he and the class speak the same language.
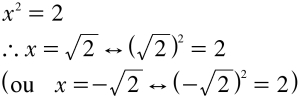
“I’m going to take a few hours this morning to tell you that that statement is ex-tra-or-di-naria [ Moses marks each syllable of the word with his right fist going up and down ]. Even today it contains mysteries! ”
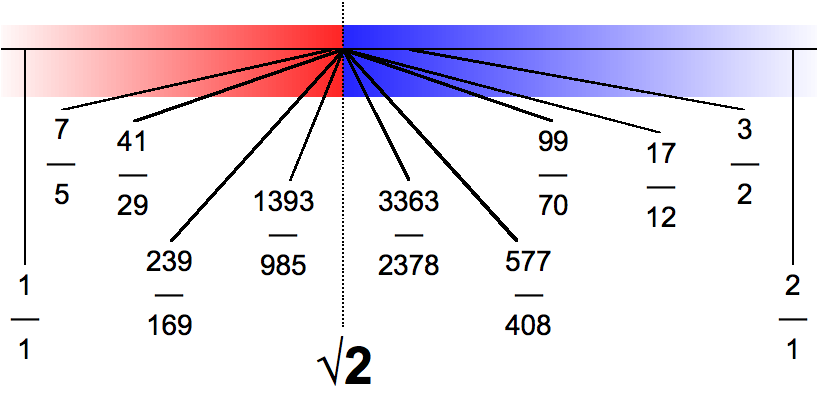
Rational sandwich . In a previous class, the class had already seen the proof that √2 is an irrational number, that is, that there are not two positive integers c and d such that c / d = √2. Then Moses shows the class how he can find the decimal places of the number x . First, it shows that 1 2 = 1 and that 2 2 = 4.
“The number x , therefore, is greater than one and less than two.”
He asks for the help of one of the students, who has a scientific calculator, and he uses this method to set up a table on the blackboard, in which the students see how the value of x is sandwiched between the values of a , always less than x , and the values of b , always greater than x .
|
The |
to 2 |
a ≤ x ≤ b |
B |
b 2 |
|
1.4 |
1.96 |
x ≊ 1.4 |
1.5 |
2.25 |
|
1.41 |
1.9881 |
x ≊ 1.41 |
1.42 |
2.0164 |
|
1,414 |
1.999396 |
x ≊ 1,414 |
1.415 |
2.002225 |
|
1.4142 |
1.99996164 |
x ≊ 1.4142 |
1.4143 |
2,00024449 |
|
1.41421 |
1.9999899241 |
x ≊ 1.41421 |
1.41422 |
2.0000182084 |
|
1.414213 |
1.999998409369 |
x ≊ 1.414213 |
1.414214 |
2.000001237796 |
|
1.4142135 |
1.99999982358225 |
x ≊ 1.4142135 |
1.4142136 |
2.00000010642496 |
Students understand that if 1.41 squared is less than 2, but 1.42 is greater, then x is between 1.41 and 1.42; if 1.414 squared is less, but 1.415 is greater, x is between 1.414 and 1.415. And so on. Moses helps them to see that they can do this process indefinitely.
“Do you see that the process is very mechanical?” Asks Moses to the class. “Do you see that we can obtain the decimal expansion of x with 20 figures, or with 500, or with 5 billion?”
It shows the class that, following the method, the numbers a and b are getting more and more equal, that is, the difference between them getting smaller and smaller. Likewise, the more decimal places the student gets, the more the 2 approaches 2 on the left, and the more b 2 also approaches 2, only on the right.
“It seems reasonable to say that this number, the root of two, exists? It seems reasonable to say that when we square the root of two, do we get two? ”
Everyone says yes, each in their own way, some with “Massa!”, Some with grunts, some staring at the blackboard fixedly and in silence.
“Now, notice something interesting. When we use a = 1.4, we are not dealing with an irrational number, but with a rational number. When we use b = 1.5, it’s the same thing. ”
Draw on the blackboard what you just said.

Moses again asks the student for help with the scientific calculator; it is the type that, when the user types a decimal number, it returns the generating fraction. The teacher, the student and the calculator come together to draw a more complete table on the blackboard.
|
The |
x |
B |
||||
|
1.4 |
1.41 |
1,414 |
√2 |
1.415 |
1.42 |
1.5 |
|
7/5 |
141/100 |
707/500 |
√2 |
283/200 |
71/50 |
3/2 |
“We can make a table like this with as many columns as we want. However, since the decimal expansion of a and b is finite, we are sandwiching x between two rational numbers. We have already seen that x is an irrational number, but all the approximations we have seen of x are rational numbers, no matter how many decimal places they have. Isn’t that strange? ”
Moses opens the roll he had put on the table; it was a huge poster. He asks for the help of four students, and the five use the masking tape to attach the poster to the board, so that everyone can see it ( figure 1 ).
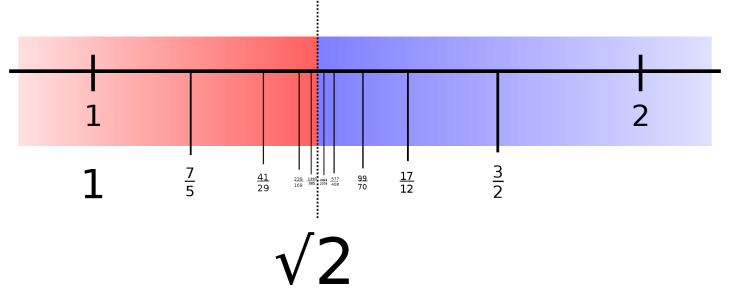
FIG. 1. A SECTION FROM DEDEKIND / WIKIPEDIA
“Note that if we continue this process for a lifetime, we will obtain a number a and a number b , both rational, such that a is less than b . We get a number a such that the second is always a little smaller than 2 and a number b such that b 2 is always a little bigger. That is why we must assume that the number √2 is between these two numbers. ”
Moses pauses, to let the class assimilate this information while looking at the figure stuck on the board.
“Now, how do mathematicians know that this number x = √2 exists? How can they be sure that, right where the number x should be , there is actually, shall we say, a little hole, an absence? How do they know that this point is not missing? How do you know, in short, that the line of real numbers is perfectly continuous? ”
The class gets into an argument and a funny guy, who has read The Hitchhiker’s Guide to the Galaxy , says the answer is “obviously 42”. Moses has fun, until he stops the racket to make an announcement.
“Guys!”, He pauses: “ mathematicians don’t know ! [ Again marks the emphasis with a closed hand .] Over the centuries, millions of people have taken millions of sticks and made millions of scratches in the sand, and after that millions of people have taken millions of pens and made millions of scratches in the notebook – because of that, because of this accumulated experience, everyone believes that a straight line is continuous, including mathematicians. But in mathematics, this belief has a name: it is the axiom of continuity. ”
Moses goes on to explain that mathematicians like questions like this, but that they take mathematics into sports. What interests them about a point is not whether it exists (“if it exists on a spiritual, metaphysical plane, look closely”), but whether they can define it precisely. In this case of the number x = √2, “defining it accurately” means determining the position of a rationale as close to √2 as necessary, be it a rationale with 5 decimal places in the decimal expansion, or a rationale with 5 trillion decimal places. Since they can determine the position of this rationale near the point x = √2, as close as they want, then, for practical purposes, that point exists – even if someone likes to think that it doesn’t exist … {❏}

{2} / Dedekind cuts
In a good elementary school (= elementary and high school), it is quite possible that the student thinks about the numbers more or less in this sequence (always using the number line as a reference): arithmetic operations with non-negative integers; arithmetic operations with non-negative fractions; arithmetic operations with integers (negative integers enter); arithmetic operations with rational numbers (negative fractions enter).
Sooner or later, like it or not, the irrational appear. Since the student does not yet have the right intellectual tools to deal with irrationals, what do most schools do? According to Hung-Hsi Wu, an American specialist in mathematics didactics, the school does not adequately discuss what an irrational number is and yet it leads the student to believe that it can handle all the numbers on the real line, including √2 or π , exactly the same way you deal with integers and rationals. This is what Wu called the Fundamental Presupposition of School Mathematics :
Fundamental Assumption of School Mathematics (PFME) . You can apply, to irrational numbers, all true information about arithmetic operations with integers and rational numbers.
“This is a very profound assumption,” writes Wu in the book Understanding Numbers in Elementary School Mathematics . “It allows the student to manipulate irrational numbers in the same way that he manipulates integers or rationals, although the student has no idea what an irrational is.”
And then there are dozens, hundreds of doubts, such as: “How do mathematicians know that numbers like √2 exist, if in no way can they know all their decimal expansion?” Or much more exotic and disabling doubts, such as: “If I have to add two weird fractions, the denominator of one is 7 and the denominator of the other is 3√5, how can I get the least common multiple between 7 and 3√5? ”
Wu is quick to say that the PFME is correct, but the school should not ask the student to believe it without first discussing it in activities similar to the one described in section 1.
The activity in section 1 was based on one of the methods with which, in college, the bachelor’s degree in mathematics builds irrational numbers: with Dedekind’s cuts .
If the reader would like to put together a Dedekind cut, here’s a brief explanation: partition all rational numbers into two disjoint sets, the set E and D . (The letters E and D serve to remind you of the left and right .) All rational smaller than certain value x are in the set E . All rational equal to certain value x , or greater than certain value x , are in the set D . In doing so, every element e of E is less than x and therefore less than every elementd of D ; and every element d to D is equal to x or greater than x and hence greater than every element and of E .
After that, the reader can take the brilliant leap that Richard Dedekind took in 1901: to define “real number” as this cut, that is, as this partition of rationals into two disjoint sets. If there is an element of D that is the smallest of all (that is, if x is rational and therefore x ∈ D ), then this cut represents the rational number x . But, if there is no element d of D that is the smallest of all (that is, if x ∉ D ), then this cut represents the irrational number x .
The whole thing is slightly more complicated than that, but Dedekind was able, with a definition similar to this, to perfectly characterize a real number. If the reader uses the definition to construct the cut relative to x = √2, he will define the sets E and D like this:
E = { and ∈ Q : e 2 <2}
D = { d ∈ Q : d 2 ≥ 2}
You can see how D cannot have an element that is the smallest of all, since x = √2 is not an element of D , because it is not rational. However, you can manipulate the cut the same way you manipulate a real number: you can very naturally add it to another cut, divide it by a cut that is not equivalent to zero, etc. (Faced with two cuts, characterized by the sets E and D , on the one hand, and E ‘ and D’ , on the other, to add the two just add each of the elements of E to each of the elements of E ‘ , and each one of the elements of D to each of the elements of D ‘. What you will get are the sets E ” and D ” , which you should define as follows: E ” = { e + e ‘ : e ∈ E e e’ ∈ E ‘ }; D ” = { d + d ‘ : d ∈ D and d’ ∈ D ‘ }. The sets E ” and D ” characterize the cut equivalent to the sum of the real number equivalent to cut E , D with the real number equivalent to cut E ‘ , D’ .)
But then you might want to know:
“Ok, I got it. But what about the value of √2? With Dedekind’s cut relative to √2 before me, how do I find the value of √2? ”
Simple: Choose any rational and the set E , or any rational d assembly D , such that and 2 or d 2 is as close as possible to 2 for its practical purposes. Hence, for your practical purposes, declare the value of √2 as the value of e or d . This was more or less what, in section 1, Professor Moisés helped the class to see.
And you might still want to know:
“Why, but does √2 exist? Wasn’t that the main question? ”
Yes there is. In mathematics, if you can define the objective criteria from which to think about a certain concept, then you can apply that concept, and obviously, if you can apply it, it exists. In essence, mathematics is the study of the logical consequences of criteria that we can objectively establish, that is, of criteria whose interpretation does not depend on the subjectivity of the reader. Since Dedekind was able to establish an objective criterion by which to describe both rational numbers and irrational numbers, then irrational numbers exist. { END }
Note :
I published the article in section 1 for the first time in the magazine Cálculo: Matemática para Todos , issue 26, March 2013, p. 16. The version you just read has been revised and rewritten. As for section 2, it is unprecedented.