Non-Euclidean Geometries
The peculiar warp observed in the Bubble World perspective and its inversive counterpart in the conformal sphere is reminiscent of non-Euclidean geometry. Three mathematicians, Karl Friedrich Gauss, Nicolai Lobaschefsky, and Janos Bolyai, each independently wondered while studying Euclid’s “Elements” why Euclid had not bothered to prove his “Fifth Postulate” with the same rigor as he had with the rest of his postulates. Essentially the “Fifth Postulate” states that if two lines that cross a third line form internal angles that sum to less than 180 degrees, then those lines must cross somewhere.

This is equivalent to the “Parallel Postulate” that parallel lines never meet, and it is also equivalent to the rule that the internal angles of a triangle sum to 180 degrees. Each of those three mathematicians set out to prove the Fifth Postulate, and all three of them failed, because although the postulate seems self-evident, it is in fact impossible to prove.
That in turn opened the possibility for non-Euclidean geometries, i.e. that it is possible to define a whole non-linear equivalent to Euclidean geometry that works in a space with positive curvature like the Bubble World perspective.

And likewise by symmetry, one that works in a space with negative curvature, like the inversive conformal world. For example the Pythagorean theorem can be demonstrated and proven in the distorted non-Euclidean spaces above just as easily as it can in Euclidean form. Euclidean geometry is a subset of a whole family of non-Euclidean geometries through a range of curvatures both positive and negative.
Gauss was genuinely disturbed that we cannot be sure that our world is truly Euclidean, it could just as well be of a non-Euclidean geometry. The perceptual model suggests that Gauss’ fear was well founded, that our “Bubble World” perspective that we see in the world around us does indeed exhibit a non-Euclidean geometry with positive curvature, and the inversive conformal world suggested by Geometric Algebra is a mirror image of that world in a space with negative curvature. The two nonlinear geometries are connected to each other and to external reality by the Euclidean geometry that they share in common.
Properties of the Conformal Model
The concentric inside-out mirroring between a central inversive conformal sphere of negative curvature, and a surrounding conformal sphere with positive curvature, offers an extraordinarily powerful system for representing geometrical form based on a very few foundational primitives.
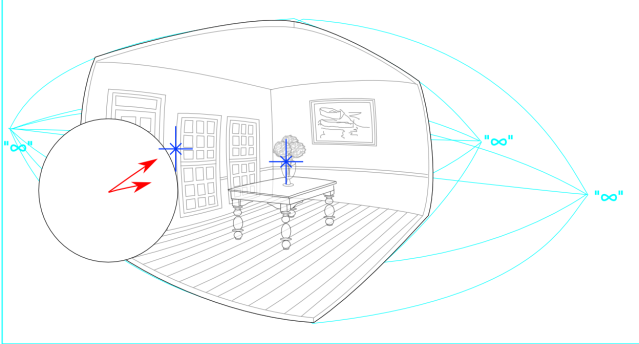
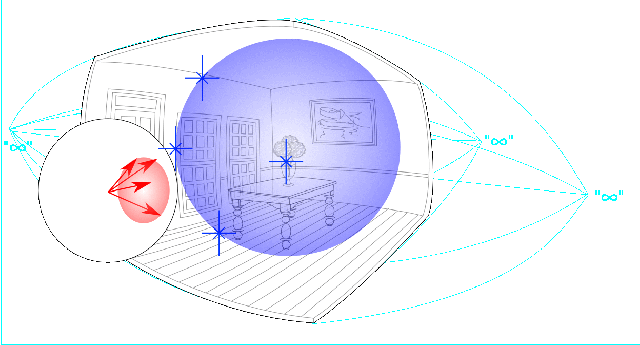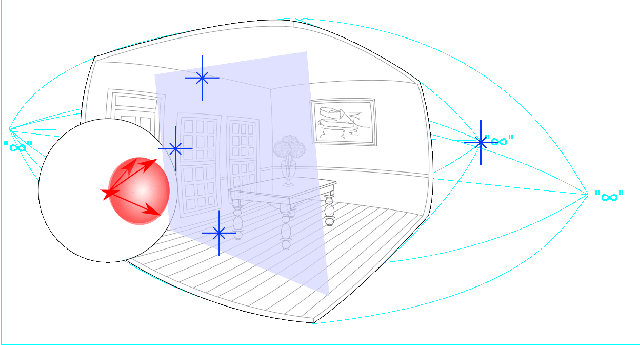
The outer Bubble World conformal mapping offers a finite bounded space capable of representing an infinite unbounded space that can now represent space all the way to infinity in all directions!
The inner inversive conformal sphere at the center can be viewed as a kind of “projection mechanism” capable of projecting geometrical images into the outer projective space based on symmetries reflected in the inner inversive space.
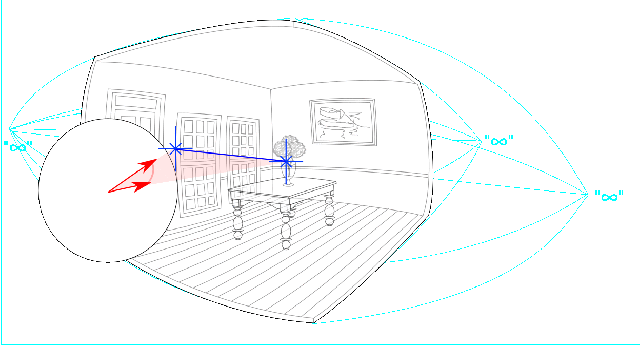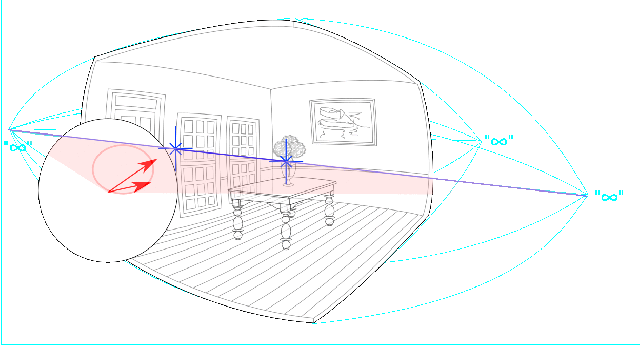
Vectors in the conformal sphere project to points in the perceptual sphere, the radial length of the vector being inversely proportional to the radial distance of the point it represents. A vector of length zero projects to “infinity” at the periphery of the perceptual space.
Two vectors presented simultaneously or successively represents two points in perceptual space.
The wedge product between two points defines the line that joins them in perceptual space. It also defines a circular arc in conformal space.
The Inner Product Null Space (IPNS) of that wedge product represents the whole line of which the line segment is a part, which completes to a full circle in the inverse conformal sphere.
This is not just a single line through the center, it can represent a range of geodesics which appear curved, but represent straight lines in that curved space.
The wedge product between three points defines the circle that joins them! Circles and straight lines are the same shape in this space.
And if one of the three points moves off to “infinity”, the wedge product defines a circle of infinite radius. A circle of infinite radius is a straight line that passes through the non-infinite points.
The wedge product between four points defines the spherical shell that passes through those four points.
And if one of those points moves off to infinity, the wedge product defines a spherical shell of infinite radius, which is a plane that passes through the three non-infinite points. Spherical shells and flat planes are the “same shape” in this space.
Here are some animations using the GAViewer (Geometric Algebra Viewer) demonstrating the principles of conformal geometry showing only the objects in external Euclidean space, although the symmetries observed in this space reflect symmetries in the inverse conformal world. (The GAViewer demonstrates Hestenes’ conformal mapping that projects back out to Euclidean space, not the conformal Bubble World space)
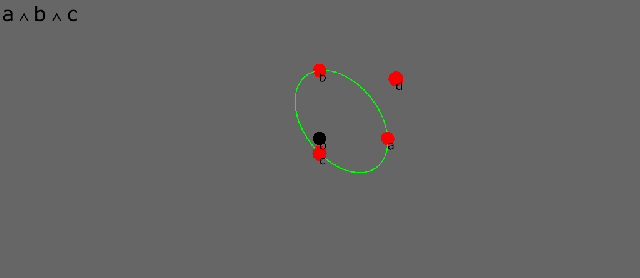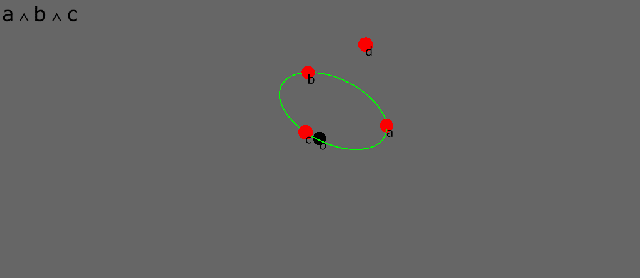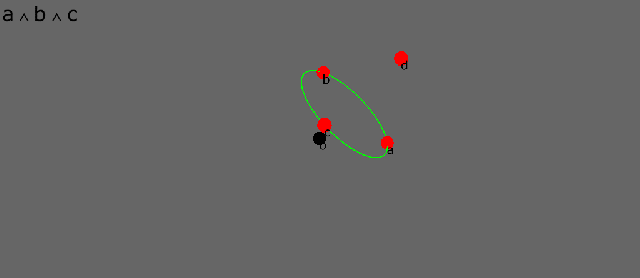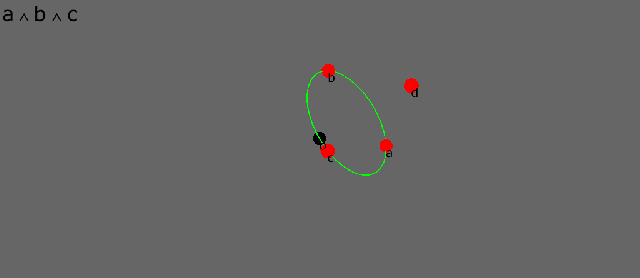
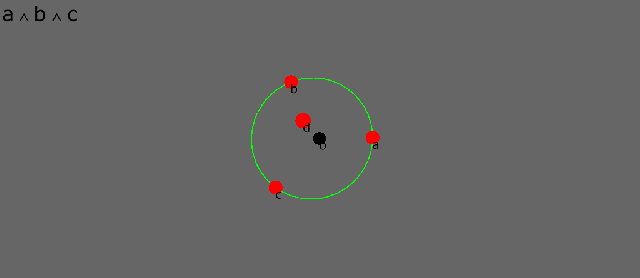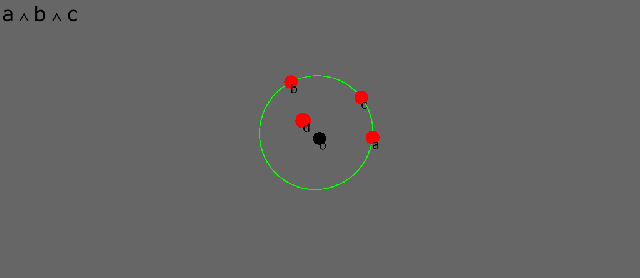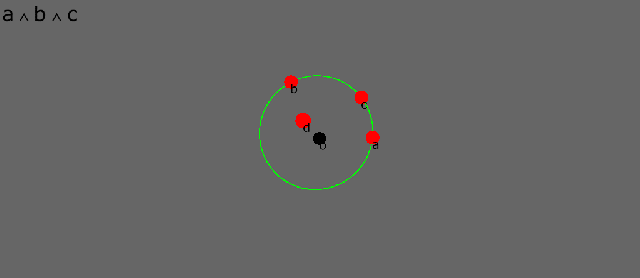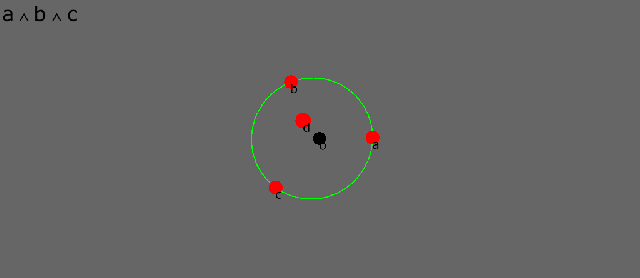
Here are four points, a, b, c, d, disposed about an (arbitrary) origin o. In conformal geometry points are dual spheres of zero radius. The dot product between two points is a scalar that is proportional to the square of the distance between them. The dot product therefore is a distance measure in conformal geometry.
The dual of a point is a sphere, and the dual of a sphere is a point. Points and spheres are the “same shape” in this space.
The wedge product between two points defines the point-pair, or line segment that joins them. Actually a point-pair is a one-dimensional sphere, i.e. two points that are equidistant from some center.
The dual of a point-pair is a circle whose radius is proportional to the separation between the two points. The dual of a circle is a point-pair.
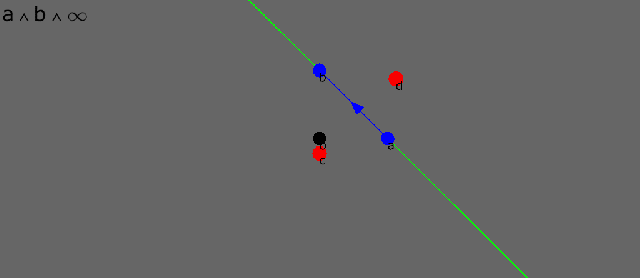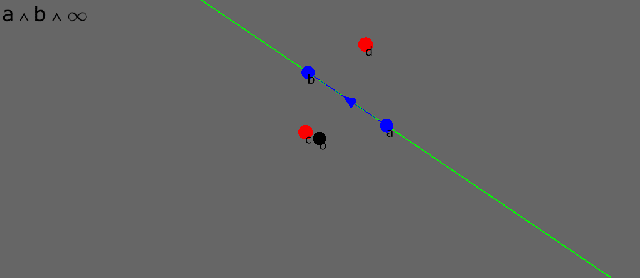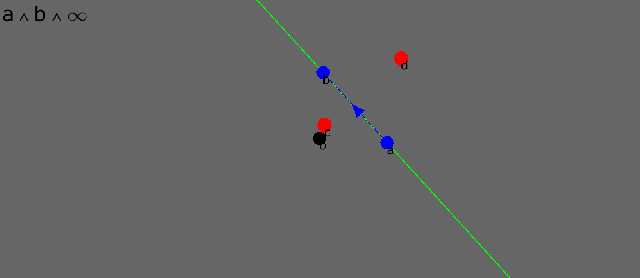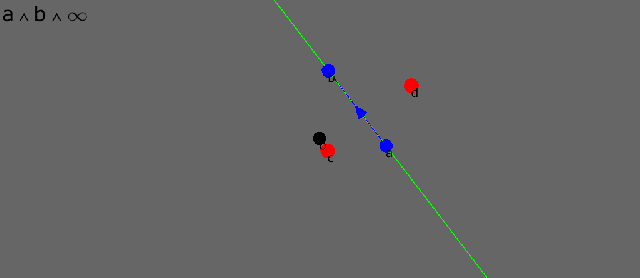
The wedge product between two points and “infinity” is the straight line containing the two points. “Infinity” is a single point that can be found in all directions.
The dual of a line is its normal plane, and the dual of a plane is its normal line.
The wedge product between three points defines the circle that joins them. This only really makes sense in the inverse conformal world where circles and straight lines are the “same shape”. It is a symmetry that shines back out to the Euclidean world.
See how the circle morphs as its defining points move. As the third point passes between the other two, the circle momentarily becomes a “circle of infinite radius”, i.e. a straight line.
The wedge product between three points and “infinity” defines the infinite plane that passes through those three points.
The wedge product between four points defines the sphere that passes through those points.
See how the sphere morphs as its defining points move. As the fourth point passes through the plane defined by the other three, the wedge product momentarily becomes an infinite plane before turning completely inside-out through “infinity”.
Closure
There are a number of curious properties of the conformal model that are a result of its circular closure.
We learned in Clifford Algebra that rotations can be expressed as double reflections. In the conformal model translation is a rotation about infinity.
Indeed all Euclidean transformations can be expressed as reflections in the conformal model! Scaling requires a reflection through a “curved mirror”, which is exactly a conformal reflection. The fact that the elements of Euclidean geometry, points, lines, planes, and spheres, are all essentially the “same shape” in conformal space, and the fact that so many Euclidean transformations can be expressed in terms of reflections is highly suggestive of a computational mechanism in the brain based fundamentally on reflections and projections between spherical elements in a conformal model.
We can now see the full implications of the principle of closure manifest at so many different levels in Geometric Algebra. Closure is not a property that makes for an accurate rendition of external reality. Closure introduces a circular warp in the representation of Euclidean space, bending straight lines into curved geodesics, and flat planes into spherical surfaces. It presents a multiplication that goes round and round instead of in and out from the origin. The purpose of closure in mathematics is the same as for the odometer, or the digital register: It provides a computational mechanism that will never “run off the edge of the page”, or roll off the end of a register, the register simply rolls back around through zero, wrapping infinity up in a finite circular reel.
There never were straight lines in the brain, the number line never extended to infinity. Like the geometry of perceptual space, the number line only approximates the linearity of the true theoretical number line, and it does so adequately only in regions relatively near the origin. It fails catastrophically at the point where it meets infinity because “infinity” falls infinitely short of true infinity at the end of the number line. Closure is what allows the mind to encompass the infinite without having to be itself infinite in extent. Closure is a practical solution to the problem of modeling an essentially infinite world in a finite bounded representation. Like the dome of the night sky, closure in mathematics is evidence of the limits and limitations of our own mind.
Conclusion
The history of Algebra has been the history of an incremental discovery of an apparently pre-existing structure. At first, the operations of mathematics were seen as convenient tricks or techniques useful for computing quantitative results. Math seemed at first to be a human invention, as individual mathematicians were credited with inventing different tricks or techniques that simplified calculations. But as more of mathematics has been revealed, the more it has become clear that mathematics is a pre-existing structure with an inherent logic of its own, and new additions to math are not arbitrary inventions, they are incremental discoveries of the hidden logic underlying mathematics. Negative numbers and the square root of minus one, it seems, were there all along waiting to be discovered, implicit in the structure of the number line and the algebraic operations on it. But if mathematics is a pre-existing structure, what is that structure, and where is it located? The time has come to finally reject the romantic notion of mathematics as an objective external entity with independent existence in an orthogonal dimension inaccessible to scientific scrutiny. The time has come to recognize mathematics for what it truly is, an artifact of the way our brain makes sense of spatial reality. Mathematics has physical existence and embodiment in the human brain. But where in the fleshy blobby grey matter of the brain would you begin to look for geometric structures like the number line? And the crystalline perfection of points and lines and planes? The brain just seems like the wrong kind of organ to express that kind of crystalline perfection.
Mathematics is not the only artifact of the computational principles of the human mind. Many have observed the intimate relationship between mathematics and music, with its geometric harmonies and periodic rhythms, and its cyclic patterns of melody, reminiscent of the rotation of a Clifford Algebra spinor.
The periodic ticks of a metronome mark out periodic intervals of time as regular as the number line. Could it be that music is yet another manifestation of the mechanism of mind? That would at least resolve the long-standing mystery of the origins and evolutionary purpose of music. And if music reveals the mechanism of mind, it also reveals mind to be composed fundamentally of oscillations. It is no accident that Clifford Algebra provides such an elegant model of cyclic oscillations, such as the spin of elemental particles. That is because Clifford Algebra is patterned on the oscillations in the human brain.
Yet another manifestation of the principles of perception is seen in ornamental art as seen churches, cathedrals, mosques, and palaces all around the world. Ornament is visual music, with its many symmetries and periodicities and crystalline perfection. If visual ornament is indeed an artifact of the computational principles of the mind, then visual ornament reveals a mechanism based on symmetries and periodicities, which are also properties of standing waves, as seen in Chladni figures obtained by bowing a steel plate with a violin bow.
Harmonic resonance is a self-organizing principle of physical matter expressed in terms of symmetries and periodicities. The complexity of the pattern that emerge far exceeds the complexity of the mechanism that produces them, which is just a homogeneous steel plate.
Below are a sample of the possible Chladni figures on a square plate and a circular plate. The circular patterns can emerge at any orientation.
Chladni figures demonstrate the basic computational principle of the brain, a principle that requires no complex mechanism besides spontaneous emergence of standing waves, a principle that is consistent with the crystalline perfection of the number line, and the concepts of points and lines and planes. And if that is not yet evidence enough for harmonic resonance in the brain, Heinrich Klüver administered LSD to volunteers who then lay in a dark room and reported their visual hallucinations. The subjects reported patterns described as grating, lattice, fretwork, filigree honeycomb, chessboard, cobweb, funnel, tunnel, cone, and spiral, that spontaneously appeared.
The patterns were exceedingly rich and complex, but each pattern appeared only for a fleeting moment before morphing endlessly into other patterns. Geometrical patterns are the primitives of visual perception.
The significance of all this symmetry to the principles of perception is revealed by psychedelic art, for example this spectacular piece called Inner Sanctum by Luke Brown inspired by the Salvia experience. If the human mind spontaneously hallucinates images so rich with symmetries and periodicities, that also suggests a harmonic resonance mechanism capable of generating hundreds of such hallucinated scenes per second.
Indeed the fact that we can instantly recognize the symmetry of a kaleidescopic pattern, is itself evidence for a symmetry-based recognition system, one that must operate in parallel to solve this intractable visual problem so rapidly.
The hyperbolic geometry of the conformal mapping is in evidence in Escher’s woodcut Circle Limit IV.
If we accept the overwhelming evidence that mathematics, music, and ornamental art are all artifacts of the computational mechanism of the brain, then we can begin to study the brain based on the properties of those artifacts. Clifford Algebra in particular suggests the operational principles of the elements of perception, or how the brain constructs geometric objects out of the basic primitives of scalars, vectors, and multivectors of higher dimension. Clifford Algebra reveals that the computational operations of the brain are explicitly spatial in nature, and that spatial nature is essential to their computational function.
The concept of duality is highly suggestive of the relationship between a standing wave oscillation as on a Chladni plate, and the nodes of that wave which are the regions where there is no oscillation. The pattern of nodes determines the shape of the vibration just as well as the vibrations themselves. For example the duality between a sphere and its central point is suggestive of a spherical standing wave oscillating between the spherical surface and its central point of symmetry.
The conformal mapping of Geometric Algebra offers a clear hint as to how a finite but explicitly spatial model can encode an essentially infinite space in a manner that seems invisible to the percipient. We have the illusion of being in a practically infinite space when outdoors, although our experience is bounded by the dome of the sky. Anything farther than that horizon is usually insignificant to our experience.
The fact that a conformal projection is itself a form of reflection, and that reflection is a most fundamental operation in Geometric Algebra suggests that the computational mechanism of the brain is built up out of simple basic elements, as are Clifford Algebra and Geometric Algebra.
The principles of phase conjugation and nonlinear optics demonstrate how a wave based system can perform computations. Whereas linear waves pass through each other transparently as if the other wave were not there, nonlinear waves warp the medium sufficient to deflect other waves, and this provides an essential control mechanism whereby one wave can modulate another, in a manner that is suggestive of a bivector formed by the wedge product between two waves, and that bivector in turn can act to deflect a third wave by Clifford multiplication. I have proposed a model of perception based on the principles of phase conjugation (Lehar).
The many phasic reversals of Clifford multiplication, and the fact that angles are represented by their projections onto the basis coordinates is suggestive of a phasic cyclic system like the Clifford Vectors Analog Electronics Analogy. I propose that the next step in investigating the computational principles of the brain would be to devise a phasic cyclic analog oscillatory model of Clifford multiplication as an image projection mechanism, capable of generating synthetic images.
The discovery of Clifford Algebra, and its subsequent elaboration into Geometric Algebra marks a profound turning point in the history of mathematics where we can finally realize what it is that we have been studying all along. When Hamilton invented his Quaternions, and Descartes plotted numbers graphically, when Gibbs invented vectors and their dot and cross products, when Herrmann Grassman invented the wedge product, unbeknownst even to themselves, these mathematical pioneers were unwittingly studying the principles of operation of the human mind implemented in the brain. Now that we know what it is we are studying in mathematics, we can begin to reverse-engineer the operational principles of our own brain under the guidance of Clifford and Geometric Algebra.