The Very Curious Little Soliton

In 1834, a man sits beside a canal. It is summer. He watches boats moving up and down the waterway. Suddenly, one boat stops abruptly and shoves a curious wave of water forward. The man stands and observes this singular wave, which passes leaving only flat water behind it. John Scott Russel stands. The wave is still moving. Disappearing from sight. He leaps on his horse. He pursues it, overtakes it, and observes it over perhaps two miles of waterway. It holds its shape, and only gradually diminishes in height. Very strange. Very curious.

Russel, an engineer, mathematician, and accomplished ship builder, was the first person to spot such a wave, follow it, and then write about it. He described called the wave a ‘wave of translation.’ Modern physics calls such singular traveling waves solitons.

What’s the big deal?

Throw a stone in a pond, and ripples spread. They spread out in concentric rings, and the rings split into more rings, and these split further. The rings begin to overlap as the taller rings overtake the shorter, and they gradually all become imperceptible as the energy of the stone spreads and is redistributed across the entire surface of the pond. Not so for the soliton. A soliton, as Russel famously chased, can travel over long distances without losing its form or its energy.

Oh, and solitons occur in not only water but light (electromagnetism) as well as in phonons (thermodynamics) and potentially in gravity waves.

You might be a soliton if:

1. You are a traveling wave in some medium
2. You hold your shape as you travel – you don’t spread out or fall apart into other waves.
3. You are a neat well defined little envelope of energy – you are not here, you arrive and pass, and then you are gone!
4. If you ever cross paths with another soliton, you can pass through each other unchanged.

Ok, what is going on with solitons?

A very very good question! How can a wave travel without dispersing or, in other words, spreading out? To answer that, there is something you should know -actually two things – about waves:

First, waves that travel through a medium tend to have ‘non linear’ velocity effects. In water this means that ‘taller’ waves travel faster than ‘shorter ones.’ In light, it means that ‘brighter’ packets of light move through glass slightly faster than ‘dimmer’ lower energy packets.

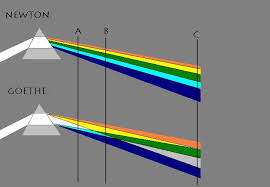
Second, as waves move through a medium, they tend to disperse, or spread out and break apart. This is essentially because higher frequency waves travel slightly slower than lower frequency waves in a given medium. A beautiful example of dispersion in light is the effect of a prism splitting white light into multiple color bands. Light entering the glass at an angle experiences a velocity change, which causes it to ‘refract’ or change course slightly. The more the light’s velocity is changed, the  greater the change in course.

 

Notice how red has been shifted fewer degrees than blue? The blue has been slowed more by the glass. In other words, glass has a slightly different ‘refractive index’ depending on color – a classic dispersive medium for light.

So again here are those two things going on:

1. Nonlinear effects based on amplitude
2. Dispersion effects based on frequency

Either one of those things by itself would pretty much scramble and spread out a random wave in a pond or a canal.  Taken together, generally speaking, they spread things out even faster.

 

 

So… imagine this:

What if there was a wave that used the effects of one to undo the effects of the other? For instance, thinking of light, what if you had a short little pulse of light that was brighter where it was bluer.  In other words, since a brighter (higher energy) pulse travels slightly faster, could it undo the fact that bluer light travels slightly slower? And if you did this, would that little pulse of light hold together and not spread out and fade away as it traveled?

Yes! It would! It would be a little soliton. 🙂

What are solitons good for?

In a word: fiberoptics. There are glass fibers laying across tens of thousands of miles of ocean floor, and somehow light going in one end still comes out the other. It’s no miracle or mistake, it happens, and because of it, so does the internet. In order to send pulses such long distances through glass fibers, special wave guides were developed to work with very specially shaped infrared light pules. IR solitons. (See bottom example in this awesome image)